Kd-Tree是一种二叉树结构,用于组织k维空间中的点集。它通过递归地将点集分割成两个子集来构建树形结构,每个节点代表一个超平面,该超平面垂直于当前维度的轴,并且通过选择一个中位数点来划分空间。这种划分方式确保了树的平衡性,从而在大多数情况下可以实现高效的最近邻搜索。
特点:
- 高效的空间划分,适用于快速查找最邻近点。
- 构建和查询的时间复杂度通常较好,但在某些特殊分布的数据集中可能会退化为线性复杂度。
- 适用于低到中等维度的数据集,在非常高维的情况下性能会下降。
由于三维点云的数目一般都比较大,所以,使用kd-tree来进行检索,可以减少很多的时间消耗,可以确保点云的关联点寻找和配准处于实时的状态。
讯享网
示例:
讯享网
运行结果
Octree
Octree是一种树状数据结构,专门用于三维空间的数据组织。它通过递归地将空间划分为八个子空间(即“八叉”)来构建。每个内部节点有八个子节点,对应于其父节点所代表的空间的八个子空间。这种结构非常适合于表示和查询具有大量空洞或稀疏区域的空间数据。

特点:
- 对三维空间进行有效的层次划分,特别适合于处理稀疏数据。
- 能够快速定位空间中的对象或点,以及进行碰撞检测等操作。
- 在需要频繁更新数据集的应用中表现良好,因为添加或删除节点相对简单。
八叉树结构通过对三维空间的几何实体进行体元剖分,每个体元具有相同的时间和空间复杂度,通过循环递归的划分方法对大小为2n*2n*2n的三维空间的几何对象进行剖分,从而构成一个具有根节点的方向图。在八叉树结构中如果被划分的体元具有相同的属性,则该体元构成一个叶节点:否则继续对该体元剖分成8个子立方体,对于2n*2n*2n大小的空间对象,最多剖分n次。
八叉树示例:
讯享网
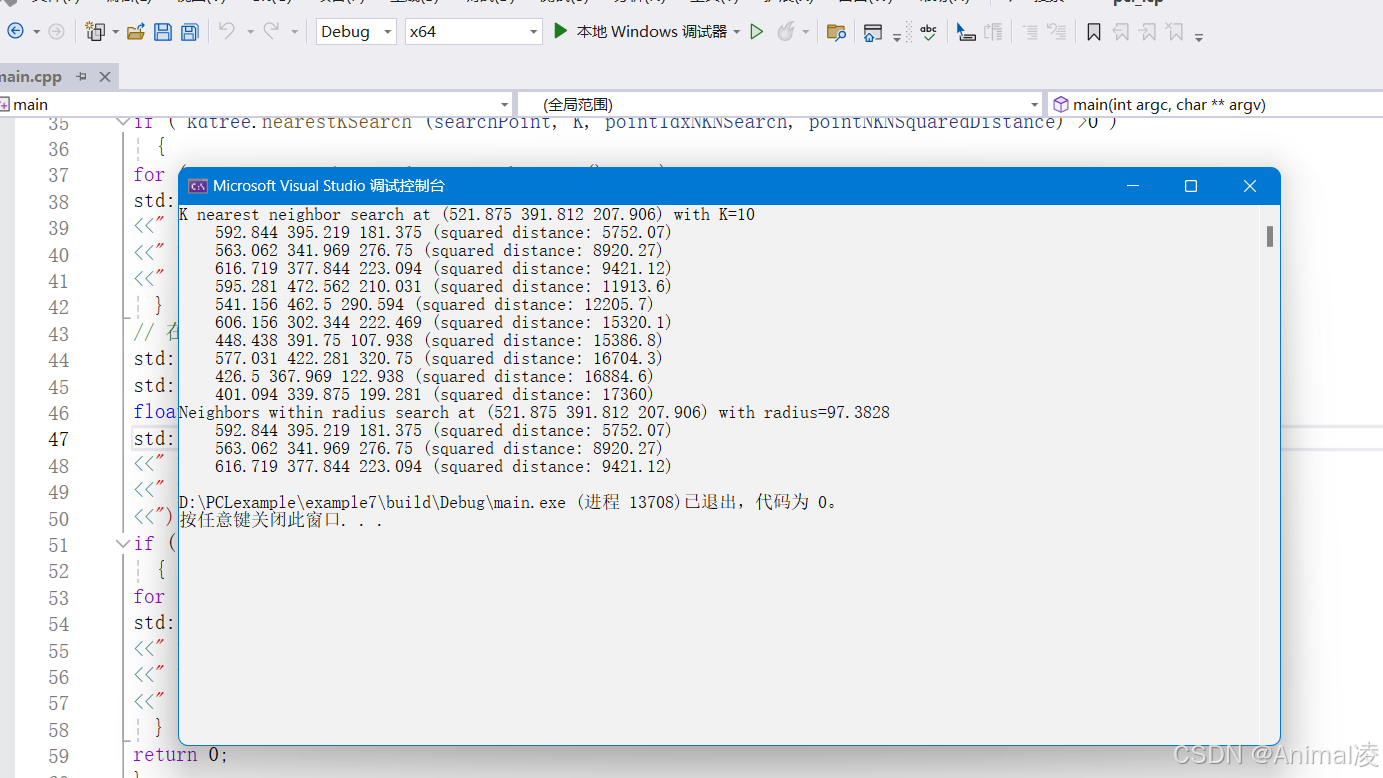
运行结果 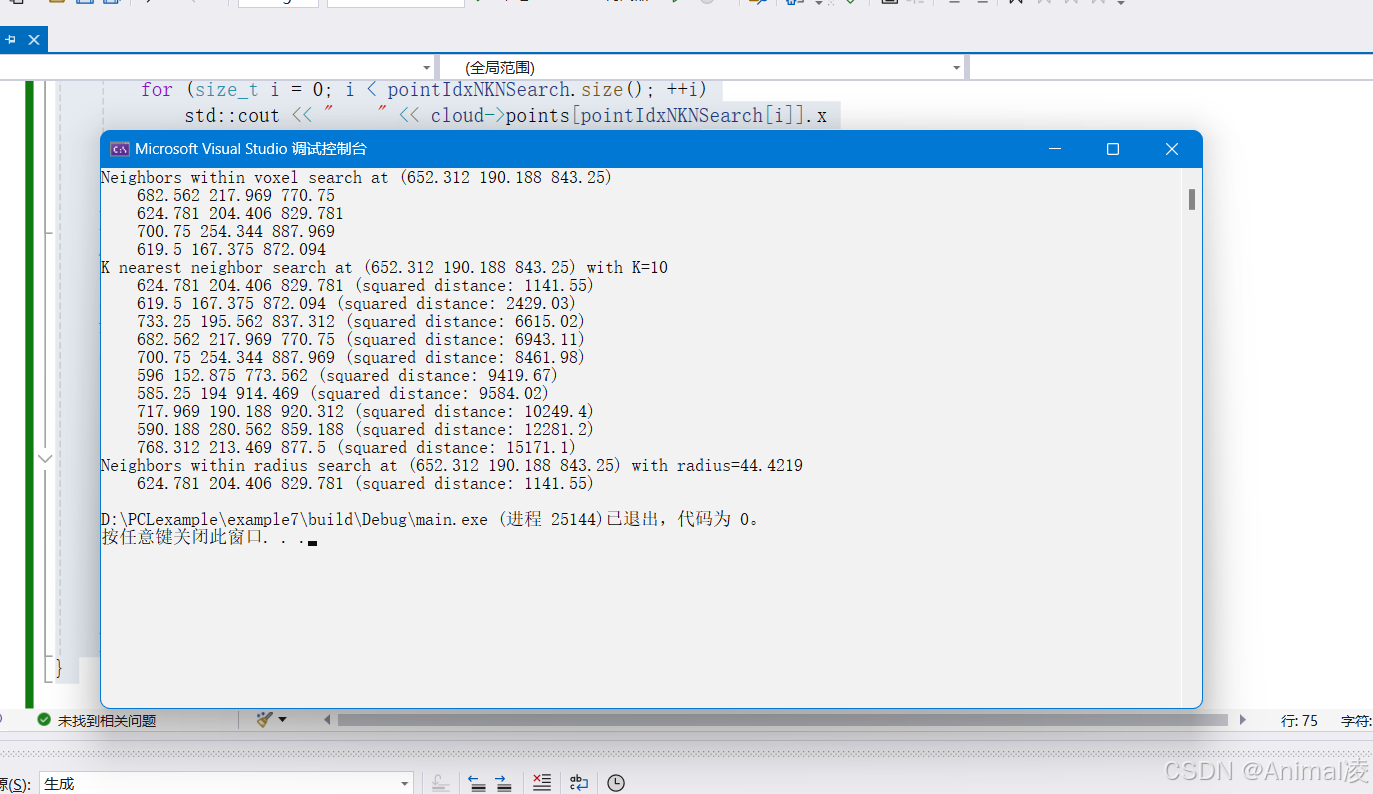
应用场景对比
- Kd-Tree 更适合于需要执行快速最近邻搜索的任务,如图像特征匹配、机器学习中的分类器等。
- Octree 则更适用于三维环境下的物体建模、场景渲染、碰撞检测等领域,尤其是在这些领域中涉及到大量空洞空间时,Octree能够更加有效地管理内存并提高查询效率。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/206866.html