前言:
在工程应用中,经常会遇到目标函数是若干个函数平方和的最优化问题。
这类问题称为最小二乘问题。
本章节讲述无约束规划中的最小二乘法。
线性最小二乘法:
当  是线性函数时,即
是线性函数时,即  ,如果令
,如果令  ,
, ,
,
则
原问题可以表示为: 
求解该方程就变成了寻找一个向量 x ,使得  达到最小。
达到最小。
如果向量  能够使得
能够使得  达到最小,即对与所有
达到最小,即对与所有  都有:
都有:

则称  为
为  的最小二乘解。当方程组
的最小二乘解。当方程组  有解时,其解自然是一个最小二乘解;若
有解时,其解自然是一个最小二乘解;若  无解,则只能寻求其最小二乘解,即能够使得 Ax 和 b 之间差值的范数达到最小的向量。
无解,则只能寻求其最小二乘解,即能够使得 Ax 和 b 之间差值的范数达到最小的向量。
下面给出两个引理:
引理1:
矩阵  ,
, ,当且仅当
,当且仅当  (即方阵
(即方阵  非奇异)时,
非奇异)时, 。
。
引理2:
能够最小化  的向量
的向量  具有唯一性。可以通过求解方程组
具有唯一性。可以通过求解方程组  得到,即
得到,即  。
。

例题分析:
例题:求线性最小二乘问题:  的最优解
的最优解
其中  ,
,
解:可以直接通过公式  判断是否有解,
判断是否有解,
 ,
,

又因为
所以:方程组 无解。
无解。
非线性最小二乘法(LM算法):
基本思想是把函数线性化,用线性最小二乘问题的解去逼近非线性最小二乘问题的解。
它通过同时利用高斯牛顿方法和梯度下降方法来解决非线性最小二乘问题。其核心思想是在每次迭
代中,根据当前参数估计计算目标函数的梯度和海森矩阵,并使用这些信息来更新模型参数。
算法步骤:
步骤1:选取初始点  ,给定初始值
,给定初始值  ,放大因子
,放大因子  ,允许误差
,允许误差  ;
;
步骤2:求出  ;
;
步骤3:求出雅克比矩阵  ;
;
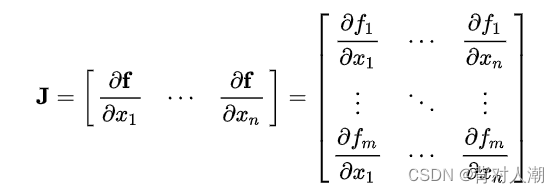

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/20181.html