2025年单向链表排序最低时间复杂度（单向链表排序最低时间复杂度怎么算）

大家好，我是讯享网，很高兴认识大家。

 <svg xmlns="http://www.w3.org/2000/svg" style="display: none;"> <path stroke-linecap="round" d="M5,0 0,2.5 5,5z" id="raphael-marker-block" style="-webkit-tap-highlight-color: rgba(0, 0, 0, 0);"></path> </svg> <p>以下笔记根据b站视频【一周刷爆LeetCode】-马士兵 总结。为个人学习记录笔记&#xff0c;特与各位学习者分享</p>

讯享网

现实比较算法流程的好坏，先看时间复杂度，时间复杂度无法比较的时候，需要根据实际运行时间来比较好坏

这两个的复杂度都是O（N^2），比较的轮数也一样，但区别是选择排序时每次把最小（或最大）的下标选出来，与最后一位进行交换。而冒泡排序是每一次比较的时候都进行交换，使最小（或最大）的逐步移位到后面

还可以理解为无进位相加
0 ⊕ N=N
N ⊕ N=0
引申---如何不引入其他变量的交换a和b的值？
答：a=a⊕b;
b=a⊕b；// 这时 b = (a ⊕ b) ⊕ b = a
a=a⊕b；// 这时 a = (a ⊕ b) ⊕ a = b
【前提：在内存里，a,b是两块独立的区域，也就是说值可以一样，但指向两个内存】

注意
不可以再数组中对相同下标的元素使用异或，因为上面的例子中，虽然值相同，但地址不同，指向的还是不同的值。而在数组中，下标相同就是同一个地址，相当于自己和自己做异或运算，而异或运算具有特性：与自身异或的结果是0，因此所有的内容都将抹为0

【使用刚才知识点的典型例题】
题目一：只有一个奇数次数的数，其余都是偶数次数
思路：让数组中所有的数异或
得到的结果就是那个奇数次的数
题目二：有两个奇数次数的数，其余是偶数次数
思路：让所有数异或，得到结果是：eor=a⊕b
假如eor的第八位是1，代表a和b在第八位一定是不一样的。
此时只异或第八位不是1的，最后得到的结果eor2是：
eor2=a 或者b

讯享网

【核心思想：把a和b以某种方式分在两个堆里】

对于

它们实际的时间复杂度是不一样的，前者O（N），后者O（N²）
但时间复杂度是按照最差的来的，因此插入排序的时间复杂度为O（N²）
【选择排序和冒泡排序的时间复杂度都是严格的O（N²），而插入排序实际的时间复杂度则不一定】

插入排序在有序数组中的操作如下：

第一步，是默认排好序的，不需要任何操作。
第二步，与前面的进行比较，由于，比较只进行一次，直接确认的位置。
第三步，与前面的比较，，只进行一次比较，确定的位置。
以此类推，每个新元素只需要进行 一次比较，因为每次比较时，新的元素总是大于前面的元素，不需要继续往前找插入位置。
因此，对于有序数组，插入排序的每次比较只需要与前一个元素比较一次，总的比较次数是 N−1次（这里 N 是数组的长度），即 线性时间复杂度 O(N)。

插入排序在逆序数组中的操作如下：
在完全逆序数组（如）中，插入排序的每个新元素需要与前面的所有元素进行比较，直到找到它应该插入的最前面位置。这导致每次插入操作都需要做大量比较，总的比较次数是 1+2+3+…+(N−1)，即形成了等差数列，总的比较次数是 O(N²)。

经典二分法
在一个有序数组中，找某个数是否存在？
答：每次都分成两部分，和这个数进行比对。时间复杂度O(log₂N)
有序数组，找>=number的最小的位置
如
每次二分的时候，先进行判断，若符合，就存下这个符合的二分的位置，若不符合，就不存，二分法把整个数组都分完的时候，箭头所指（即存下的位置）就是符合条件的值。
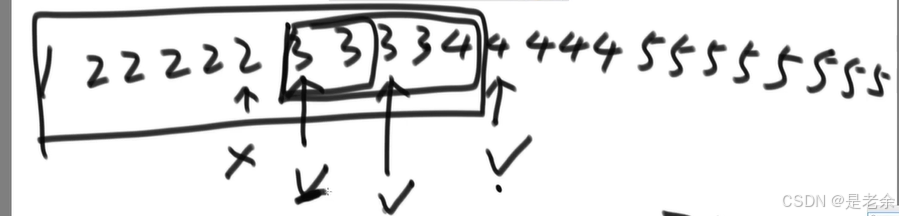
在这里插入图片描述

【经典二分法和这个的最大区别就是，前者，只要找到这个数就不再二分了，而后者，==要一直分到最后为止==】

局部最小：比如有个数i，比i-1小，也比i+1小，不用考虑其他的，它就是一个局部最小的数。

在这里插入图片描述

【解题思路为：二分法变形】
解答：先看第一个，如果第一个是局部最小，那直接返回了，如果不是，那么它的趋势一定是降低的。
再看N-1项，如果它是局部最小，也直接返回。如果不是，证明N-1往前的趋势也是降低的。
如果0与N-1都不是局部最小，那么直接二分法取中间，如果是局部最小，就返回。如果不是（比如M比M-1要大）那么在0到M中间，必有局部最小。二分到最后，一定能找到至少一个局部最小的值。
【不一定必须有序才要用到二分，根据题目的状况与策略，有时也是会用到二分。左右两侧和策略有关，并且确定可以甩掉一边，就可以使用二分】

比如上道题，用二分法做的这种方法为方法a（这个方法不确定对不对）
写一个不追求时间复杂度的算法，一定确定对的方法，为方法b
这两个方法，通过随机数模拟测试几千次（或更多），判断两个结果是否相等，从而确定方法a是否正确。

2025年单向链表排序最低时间复杂度（单向链表排序最低时间复杂度怎么算）

相关推荐