alpha 是 选择为 50/ k, 其中k是你选择的topic数,beta一般选为0.01吧,,这都是经验值,貌似效果比较好,收敛比较快一点。。有一篇paper, lda-based document models for ad-hoc retrieval里面的实验系数设置有提到一下啊
一.主题模型的引入
主题模型是一个统计模型,用来抽离出一批文档中的“主题”。直觉上,已知一篇文档的一个特定主题,则我们有理由相信一些词会更可能出现在这篇文档,“狗”和“骨头”更有可能出现在一篇有关于狗的文档中,“猫”和“喵”更有可能出现在有关于猫的文档中,而英语当中的“the”和“is”在这些文档中出现的概率相当。一般来说一篇文档都含有多个主题,这些主题之间所占比例有所不同,一篇文档10%是有关猫90%有关狗,那么这篇文档“狗”这个词出现的次数可能会是“猫”的9倍。
如果上边的说法还不够形象,下边有两句话:
“马云、马化腾和李彦宏”
“阿里巴巴、腾讯和百度掌门人”
如果按照jaccard距离来表征两句话的相似性,将会得到两句话完全不相干的错误结论,这显然是不对的。但是一进行语义分析才发现这两句话其实说的完全一回事。或者更准确的说,在这里把两句话的主题抽离出来,将会得到“企业家”、“互联网”、“BAT”等等这些主题,这样就发现两句话主题上是完全相同的,由此可知这两句话具有很高的相似性。
主题模型中的主题实际就是一个标签,用这个标签尽最大可能去概括一段话或一篇文档的内容。这里有点类似小学时候经常被老师要求“总结中心思想”的作用,主题在这里就是“中心思想”。但又不仅仅是“中心思想”,数学上的主题模型更像一个语料库,在这个语料库里每一个词都有一个对应的概率分布去表征这个词的出现,在特定的主题里边,有些词出现概率高,另外一些词出现概率低,比如上边的主题是“狗”的文档中,“骨头”出现的概率就要比“喵”高。
二.数学解释
主题模型就是用来对文档建模的数学工具,它是一个生成模型,何谓生成模型,就是要求得目标概率,必须先通过求联合概率,然后再利用概率运算公式得到。一般符合下式:

讯享网
其中, 是要求的结果,表示给定输入量,输出关于输入的概率分布。
是要求的结果,表示给定输入量,输出关于输入的概率分布。
从上式中可以明显看到生成模型的结果并不是直接从数据中得到的,它有一个中间过程。
而判别模型则不同,完全省掉了中间求联合概率的步骤,直接从数据训练样本中学习最终所要预测的概率,即 。 (当然,这里是针对概率模型而言,另一种是非概率模型,那就相应的是直接从训练样本中学习到决策函数F(X)的是判别模型.)
。 (当然,这里是针对概率模型而言,另一种是非概率模型,那就相应的是直接从训练样本中学习到决策函数F(X)的是判别模型.)
回到主题模型,在主题模型的框架里,每一篇文档的产生都遵循着这样一个步骤:每一篇文档都有一系列主题,这些主题共同符合一定的概率分布(当然不同文档的主题概率分布不尽相同),依据这个概率分布随机选择一个主题,然后再从这个主题里按照另一个概率分布选择一个词。这个词就是文档的第一个词,其余的词都是这个过程。用公式来表示就是:
P(词|文档)= P(词|主题)P(主题|文档)
P(词|主题)P(主题|文档)
(吐个槽,知乎的编辑器真是蛋疼,中文都不能显示在编辑器中,注意那个求和符号是对主题进行求和)
其实,这个式子的更准确表示形式应该是:
P(词|文档)
= P(词,主题|文档)
P(词,主题|文档)
= P(词|主题,文档)P(主题|文档)
P(词|主题,文档)P(主题|文档)
= P(词|主题)P(主题|文档)
P(词|主题)P(主题|文档)
对于最后一个等式的成立,我认为是近似了的,这是我个人的想法,不知道对不对,求高人指正。
从上述的运算过程中,我们可以明确的知道P(词|文档)的得到是通过一系列运算得到的,并不是直接从训练数据样本中得到的,所以说主题模型是一个生成模型。
矩阵表示形式是:
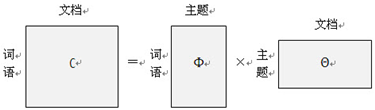
主题模型有很多方法,主要有两种:pLSA(Probabilistic latent semantic analysis)和LDA(Latent Dirichlet allocation)。下面主要对这两种方法展开来讲。
三.Probabilistic latent semantic analysis
pLSA的另一个名称是probabilistic latent semantic indexing(pLSI),假设在一篇文档d中,主题用c来表示,词用w来表示,则有如下公式:
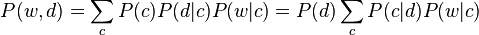
第一个等式是对称形式,其主要思路是认为文档和词都按照一定的概率分布(分别是P(d|c)和P(w|c))从主题c中产生;第二个等式是非对称形式,更符合我们的直觉,主要思路是从该文档中按照一定概率分布选择一个主题(即P(c|d)),然后再从该主题中选择这个词,这个概率对应是P(w|c),这个公式恰好和上文所讲的一致。即把这里的非对称形式的公式左右都除以P(d)便得到下面这个公式:
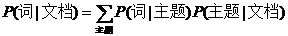
用盘子表示法(英语是Plate notation,不知道翻译对不对)如下:
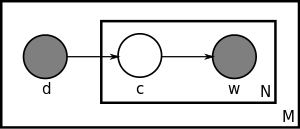
最大的矩形(盘子)里装有M个小盘子,即有M篇文档,每一篇文档d自身有个概率P(d),从d到主题c有一个概率分布P(c|d),随后从主题c到词w又是一个概率分布P(w|c),由此构成了w和c的联合概率分布P(w,d).
pLSA的参数个数是cd+wc,所以参数个数随着文档d的增加而线性增加。但是很重要的的是,pLSA只是对已有文档的建模,也就是说生成模型只是适合于这些用以训练pLSA算法的文档,并不是新文档的生成模型。这一点很重要,因为我们后文要说的pLSA很容易过拟合,还有LDA为了解决这些问题引入的狄利克雷分布都与此有关。 (In addition, although PLSA is a generative model of the documents in the collection it is estimated on, it is not a generative model of new documents.
The LDA model is essentially the Bayesian version of PLSA model. The Bayesian formulation tends to perform better on small datasets because Bayesian methods can avoid overfitting the data. For very large datasets, the results of the two models tend to converge. 两段话都摘自维基百科)
四.Latent Dirichlet allocation
在LDA中,每一篇文档都被看做是有一系列主题,在这一点上和pLSA是一致的。实际上,LDA的不同之处在于,pLSA的主题的概率分布P(c|d)是一个确定的概率分布,也就是虽然主题c不确定,但是c符合的概率分布是确定的,比如符合高斯分布,这个高斯分布的各参数是确定的,但是在LDA中,这个高斯分布都是不确定的,高斯分布又服从一个狄利克雷先验分布(Dirichlet prior),说的绕口一点是主题的概率分布的概率分布,除了主题有这个特点之外,另外词在主题下的分布也不再是确定分布,同样也服从一个狄利克雷先验分布。所以实际上LDA是pLSA的改进版,延伸版。
这个改进有什么好处呢?就是我们上文说的pLSA容易过拟合,何谓过拟合?过拟合就是训练出来的模型对训练数据有很好的表征能力,但是一应用到新的训练数据上就挂了。这就是所谓的泛化能力不够。我们说一个人适应新环境的能力不行,也可以说他在他熟悉的环境里过拟合了。
那为什么pLSA容易过拟合,而LDA就这么牛逼呢?这个要展开讲,可以讲好多好多啊,可以扯到频率学派和贝叶斯学派关于概率的争论,这个争论至今悬而未决,在这里,我讲一下我自己的看法,说的不对的,希望指正。
pLSA中,主题的概率分布P(c|d)和词在主题下的概率分布P(w|c)既然是概率分布,那么就必须要有样本进行统计才能得到这些概率分布。更具体的讲,主题模型就是为了做这个事情的,训练已获得的数据样本,得到这些参数,那么一个pLSA模型便得到了,但是这个时候问题就来了:这些参数是建立在训练样本上得到的。这是个大问题啊!你怎么能确保新加入的数据同样符合这些参数呢?你能不能别这么草率鲁莽?但是频率学派就有这么任性,他们认为参数是存在并且是确定的, 只是我们未知而已,并且正是因为未知,我们才去训练pLSA的,训练之后得到的参数同样适合于新加入的数据,因为他们相信参数是确定的,既然适合于训练数据,那么也同样适合于新加入的数据了。
但是真实情况却不是这样,尤其是训练样本量比较少的情况下的时候,这个时候首先就不符合大数定律的条件(这里插一句大数定律和中心极限定律,在无数次独立同分布的随机事件中,事件的频率趋于一个稳定的概率值,这是大数定律;而同样的无数次独立同分布的随机事件中,事件的分布趋近于一个稳定的正态分布,而这个正太分布的期望值正是大数定律里面的概率值。所以,中心极限定理比大数定律揭示的现象更深刻,同时成立的条件当然也要相对来说苛刻一些。 非数学系出身,不对请直接喷),所以频率并不能很好的近似于概率,所以得到的参数肯定不好。我们都知道,概率的获取必须以拥有大量可重复性实验为前提,但是这里的主题模型训练显然并不能在每个场景下都有大量的训练数据。所以,当训练数据量偏小的时候,pLSA就无可避免的陷入了过拟合的泥潭里了。为了解决这个问题,LDA给这些参数都加入了一个先验知识,就是当数据量小的时候,我人为的给你一些专家性的指导,你这个参数应该这样不应该那样。比如你要统计一个地区的人口年龄分布,假如你手上有的训练数据是一所大学的人口数据,统计出来的结果肯定是年轻人占比绝大多数,这个时候你训练出来的模型肯定是有问题的,但是我现在加入一些先验知识进去,专家认为这个地区中老年人口怎么占比这么少?不行,我得给你修正修正,这个时候得到的结果就会好很多。所以LDA相比pLSA就优在这里,它对这些参数加入了一些先验的分布进去。(但是我这里并没有任何意思说贝叶斯学派优于频率学派,两学派各有自己的优势领域,比如很多频率学派对贝叶斯学派的攻击点之一是,在模型建立过程中,贝叶斯学派加入的先验知识难免主观片面,并且很多时候加入都只是为了数学模型上运算的方便。我这里只是举了一个适合贝叶斯学派的例子而已)
但是,当训练样本量足够大,pLSA的效果是可以等同于LDA的,因为过拟合的原因就是训练数据量太少,当把数据量提上去之后,过拟合现象会有明显的改观。
五.LDA的具体数学形式
在正式讲LDA的数学模型之前,先讲两个比较基础的模型。
1.Unigram model
每一篇文档的概率是组成这篇文档所有词的概率之乘积。表示如下:
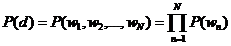
实际上,正确的推导应该是
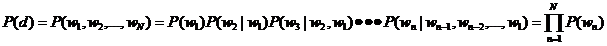
最后一步里,把概率的计算进行了简化,粗暴地认为词与词之间没有联系。盘子表示法如下:
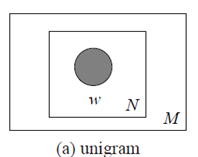
M篇文档,每一篇文档有N个词,词与词之间是相互独立存在的。
2.Mixture of unigrams
Unigram model 没有主题,文档直接被分解成词,而Mixture of unigrams 模型则给文档一个主题,并且从这个主题中去按照一定概率分布去选择所需要的词。图模型如下:
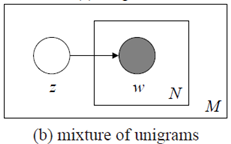
用数学公式来表示就是
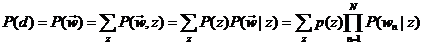
也就是说,主题z在这里是一个隐变量,但需要注意的是,虽然要对z求和,但是表示的意思却是每篇文档却只有一个主题。
3.LDA
终于要讲到LDA了,其实弄清楚上述这些基本模型之后,LDA就是水到渠成的事情了,因为Mixture of unigrams模型只有一个主题,这显然不符合实际情况,一篇文档很有可能包含多个不同的主题,而这些主题服从一个概率分布,用
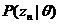
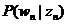
也服从一个狄利克雷分布,用
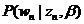
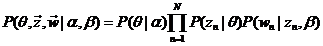
其中,α和β是dirichlet的参数,对于M篇文档都一样,用来控制每篇文档的两个概率分布;θ对于每一篇文档都一样,用来表征文档的主题分布;z是每个词的隐含主题,w是文档里的词。图模型如下:
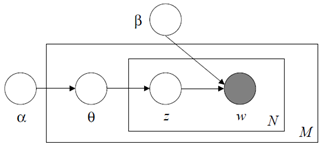
从图中可知,α和β是文集(corpus)级别的参数,所以在M篇文档外边,θ是文档级别的参数,在N个词盘子的外边,z和w是一一对应的,每个词对应一个隐含主题。
下边这个图是个神图,怎么都能如此机智呢?把这些复杂隐晦的关键点全都形象的图形化了,不得不佩服。
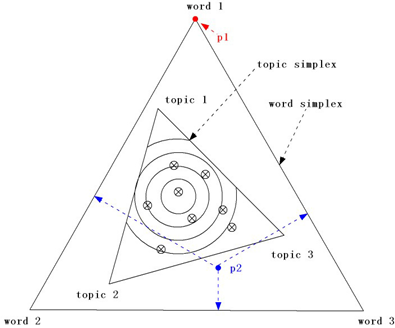
首先,我们假设一篇文档含有3个词,待选主题也是3个,为什么选择3?主要是是为了好用三角形来表示他们的关系,当然如果你有很好的超空间想象能力,你也可以选择更多的词来描述。
外边最大的三角形是word simplex,其内的每一个点都表示一个概率分布,也就是产生这三个词的概率大小。比如p2这个点,它产生word 1的概率是,p2点到word 1对边的距离,也就是p2到底边的距离。由于等边三角形内的任何一点到三条边的距离之和等于高,相当于概率之和为1类似,这就非常好的保证了用距离来度量概率大小的准确性。
小三角形是topic simplex,其内的每一个点表示产生这三个topic的概率分布,和word simplex类似。三个顶点,比如topic1由于它在word simplex内部,所以表示的意义是:由topic1产生三个word的概率分布,即前文公式里的
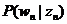
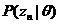
我们再来看看Mixture of unigrams如何表示在图形中,由于该模型只有一个主题,所以随机在三个主题中,选择一个,假如是topic1,然后再按照topic1到各边的距离(也就是产生各个词的概率大小)来生成3个词。这样整个文档便生成了。在图形中表示就是Topic simplex三个顶点上的随即一个点便是Mixture of unigrams模型。
pLSA的主题不止一个,表示成为Topic simple图里的带叉的点,每个带叉的点便是一个pLSA模型,产生文档的时候,先按照带叉点到Topic simple三条边距离来选择一个主题,然后再按照Mixture of unigrams的形式来选择三个词当中的一个,有几个隐含主题就按照这种方式选几个主题,然后再通过这些主题去产生下一步的词。
LDA相对pLSA的变化就是,它不再仅仅是Topic simple图里的带叉的点,而是一条曲线,一个点表示topic的一个概率分布,虽然topic是有一定随机性的,但是topic的分布不具有随机性,而是确定的点,但现在LDA不仅topic是随机的,topic的分布也是随机性的,所以表现出来就不再是一个确定的点,而是一系列的点,这条曲线由上文中的狄利克雷分布的参数α和β来确定,也就是
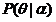
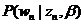
有些人会问,为什么非得要用dirichlet分布呢?对,还真有用其他分布的,比如 logistic normal distribution等等,这些相当于都是LDA的变形,不做过多讨论,感兴趣的可以查阅相关文献。
既然模型已经解释的这么透彻了,那么如何利用数据样本训练出这个模型呢?这里就有很多的数学运算了,基本思路是:由于在文档里,唯一的观察量(也就是模型的输入变量)是词w,w是一个向量,另外已知的是dirichlet分布的参数α和β,其他的都是隐变量,而对于隐变量的最好工具便是EM算法,通过极大化所求目标量的下界来逐步逼近目标量的极大值。具体的数学细节若有时间我再来更新。
最后,就是LDA的应用啦,当然最主要的是文档主题,背后语义的分析等等,当然我们可以将LDA适当做一些变形之后利用到图形处理等领域,把图片当做一个文档,其内的像素点当做一个个词,Deep Learning对于图形的处理已经证明了像素点往上层抽象可以组成一些基本单元,我们可以类似到这里作为主题。(这是我自己瞎诌的,不知道对不对,高手请尽情喷)
最后的最后,希望大家踊跃提出文中的错误,先谢谢各位啦!
参考资料:
1.Topic model
2.Probabilistic latent semantic analysis
3.Latent Dirichlet allocation
4.主题模型-LDA浅析
5.【JMLR’03】Latent Dirichlet Allocation (LDA)
6.http://jmlr.csail.mit.edu/papers/v3/blei03a.html (LDA的创世纪文章)
共轭分布(conjugate distribution)与共轭先验(conjugate prior),其实是两个非常也有意思的概念。
在说共轭分布共轭先验之前,我们先说说什么是共轭。
首先应该你可以记得起来的应该是复数的定义中:

为什么它两被称为共轭呢?
因为它两如果在复平面上表示的话,关于实轴对称!所以我们的直观理解就是
共轭是某种意义上的“对称”!
接下去,或许你还会想起的是一个叫共轭双曲线的东西,即下面那个东东
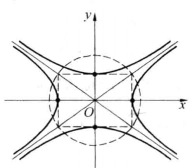
看着图,应该可以找到两组双曲线吧?说到双曲线或许高中的小伙伴应该不陌生吧,刻画双曲线的几个重要量,焦点,渐近线,离心率。在这个图中我们可以看到,
它们共渐进线,它们的焦点都在一个圆上,他们的离心率的倒数的平方和等于1.
因而他们有相同的地方,他们也有不同的地方。所以在这里共轭直观的理解可以是
共轭描述的某些重要指标相同,某些量互补。
在下面如果你了解矩阵就应该知道矩阵中也有个非常重要的共轭概念–共轭矩阵,或者说是自共轭矩阵也叫Hermite阵,即矩阵的第i行第j列都与第j行第i列共轭相等(按照复数的共轭定义):

比如,这样的一个矩阵:
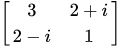
观察一下这个矩阵,应该可以想到一个共轭矩阵的主对角线必然是实数,因为  那么b肯定只能是0。另外所有实对称矩阵自然都是共轭矩阵啦,对不?这里的共轭矩阵会带来很多优秀的性质。在这里,我们可以直观的理解是:
那么b肯定只能是0。另外所有实对称矩阵自然都是共轭矩阵啦,对不?这里的共轭矩阵会带来很多优秀的性质。在这里,我们可以直观的理解是:
共轭会保证一些优秀的性质,以便于之后的分析计算。
其实看到上面这一些的共轭,大家应该对共轭这个词语有了一定的了解。现在我们来说说分布意义上的共轭。既然这个数字可以有共轭,曲线可以有共轭,矩阵可以有共轭,那么分布为什么不能有共轭呢?说到这个分布意义下的共轭,必然离不开那个经典的贝叶斯推断的公式:
后验 = 先验 * 似然!
首先说说这三者的关系,任意一个模型都是有observation和参数构成的吧。区别于频率学派,贝叶斯的世界中,所有的参数并不是一个固定的数字,而是一个个的随机变量,既然是随机变量,那么我们自然可以假定(或者根据经验要求)其来自某一个已知的性质良好的概率分布,对吧?这个概率分布我们称之为“先验prior distribution”。
那什么是似然呢?
The likelihood function(often simply called the likelihood) describes the joint probability of the observed dataas a function of the parameters of the chosen statistical model.[
似然是我们认定的,用来描述观测值在给定参数的时候的联合分布的概率!这是个既定事实,这代表了我们对于这个问题的看法,一般的模型建立后就不会去更改。你肯定了它的likelihood是高斯的那么它一直都是高斯的。
那什么是后验呢?后验就是根据你给出的prior和确定下来的likelihood,由贝叶斯公式计算出来的东西。它表示了大家对于参数的看法在给定observation之后的更新!这些都是贝叶斯统计的基础内容,相信大家已经看过好多的文章介绍了吧,这里就不多叙述啦!
那什么是共轭分布(conjugate distribution)呢?
In Bayesian probability theory, if the posterior distribution p( θ | x) is in the same probability distribution family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions,and the prior is called a conjugate priorfor the likelihood function p(x | θ).
即,先验与后验来自于同一个族的概率分布。
为什么说是同一个族的概率分布而不是同一个概率分布呢?
因为即便是高斯分布,mean或者variance一变,自然就是不同的分布了哈!这个先验算上likelihood自然不可能跟后验是exact same distribution啦,那么自然只能退而求其次,同一个类型的分布啦!即先验是高斯分布的,给定某个likelihood下,后验也是高斯分布,那么我们就叫这个两个分布是共轭分布,这个先验叫做是基于这个给定的likelihood下的共轭先验。
比如一般假定高斯的likelihood(一直variance,模型参数只有mean)下,高斯分布的共轭分布还是高斯(当然这里其实还有好多好多的情况, 详情请见:https://en.wikipedia.org/wiki/Conjugate_prior)。从形式上来讲,即

其中一个高斯的密度函数乘以一个高斯的密度函数,无视系数的情况下还是可以写成一个高斯密度函数的形式!
其实仔细想来,这样的分布意义下的共轭是不是也挺满足一般意义下共轭的说法呢?
1。 对称。 emmmm, 如果把likelihood看做是一个实轴一样的东西,那其实这不就是两个分布在依赖于likelihood的情况下,翻过来翻过去吗?
2。 有些相似有些不同。相似的是他们都具有相同的分布族,对吧?不同是是在贝叶斯统计中,一个位于prior的位置,另一个位于posterior的位置上。是不是也有些像那个双曲线的图呢?一组是左右的,一组是上下的,但是他们共用渐近线和焦点都在同一个圆上呢?
3。保证优秀的性质。这点其实才是最为核心的原因,当然也是最实用的哈!
为什么呢?因为贝叶斯统计所操作是整天都是prior,likelihood,posterior,对吧?如果先验和后验同属一个分不族,计算上自然是好很多,可以大大简化很多的计算过程。另外,一旦是共轭分布,那么在很多需要积分的地方则可以直接给出显式的数学表达式,而不需要使用数值方法去计算!
同时,不计算的情况下,也可以为贝叶斯统计推断提供一些最为直观快速的inspiration!
高中数学考试及学习技巧高中数学必备的88个基础公式(多图)因为MPI在可扩展性上的限制, 我们可以大致理解为什么Google的并行计算架构上没有实现经典的MPI。同时,我们自然的考虑Google里当时最有名的并行计算框架MapReduce。
MapReduce的风格和MPI截然相反。MapReduce对程序的结构有严格的约束——计算过程必须能在两个函数中描述:map和reduce;输入和输出数据都必须是一个一个的records;任务之间不能通信,整个计算过程中唯一的通信机会是map phase和reduce phase之间的shuffuling phase,这是在框架控制下的,而不是应用代码控制的。
pLSA模型的作者Thomas Hoffmann提出的机器学习算法是EM。EM是各种机器学习inference算法中少数适合用MapReduce框架描述的——map phase用来推测(inference)隐含变量的分布(distributions of hidden variables),也就是实现E-step;reduce phase利用上述结果来更新模型参数,也即是M-step。
但是2008年的时候,pLSA已经被新兴的LDA掩盖了。LDA是pLSA的generalization:一方面LDA的hyperparameter设为特定值的时候,就specialize成pLSA了。从工程应用价值的角度看,这个数学方法的generalization,允许我们用一个训练好的模型解释任何一段文本中的语义。而pLSA只能理解训练文本中的语义。(虽然也有ad hoc的方法让pLSA理解新文本的语义,但是大都效率低,并且并不符合pLSA的数学定义。)这就让继续研究pLSA价值不明显了。
另一方面,LDA的inference很麻烦,没法做精确inference,只有近似算法,比如variational inference。如果EM算法中的E-step采用variational infernece,那么EM算法就被称为variational EM。EM本来就是一个比较容易陷入局部最优的算法,E-step用了variational inference,总体效果就更差了。另一种近似inference算法是Gibbs sampling。虽然我们可以在E-step里用Gibbs sampling替换variational inference,但是Thomas Griffiths发现一个有趣的特点——稍微修改LDA之后,就可以利用Dirichlet和multinomial分布的共轭性,把模型参数都积分积掉。没有参数了,也就所谓M-step里的“更新参数”了。这样,只需要做Gibbs sampling即可。这个路子发表在PNAS上,题目是Finding Scientific Topics。
Gibbs sampling也有一个问题:作为一种Markov Chain Monte Carlo(MCMC)算法,顾名思义,Gibbs sampling是一个顺序过程,按照定义不能被并行化。幸运的是,2007年的时候,UC Irvine的David Newman团队发现,对于LDA这个特定的模型,Gibbs sampling可以被并行化。具体的说,把训练数据拆分成多份,用每一份独立的训练模型。每隔几个Gibbs sampling迭代,这几个局部模型之间做一次同步,得到一个全局模型,并且用这个全局模型替换各个局部模型。这个研究发表在NIPS上,题目是:Distributed Inference for Latent Dirichlet Allocation。
上述做法,在2012年Jeff Dean关于distributed deep leearning的论文中,被称为data parallelism(数据并行)。如果一个算法可以做数据并行,很可能就是可扩展(scalable)的了。
David Newman团队的发现允许我们用多个map tasks并行的做Gibbs sampling,然后在reduce phase中作模型的同步。这样,一个训练过程可以表述成一串MapReduce jobs。我用了一周时间在Google MapReduce框架上实现实现和验证了这个方法。后来在同事Matthew Stanton的帮助下,优化代码,提升效率。但是,因为每次启动一个MapReduce job,系统都需要重新安排进程(re-schedule);并且每个job都需要访问GFS,效率不高。在当年的Google MapReduce系统中,1/3的时间花在这些杂碎问题上了。后来实习生司宪策在Hadoop上也实现了这个方法。我印象里Hadoop环境下,杂碎事务消耗的时间比例更大。
随后白红杰在我们的代码基础上修改了数据结构,使其更适合MPI的AllReduce操作。这样就得到了一个高效率的LDA实现。我们把用MapReduce和MPI实现的LDA的Gibbs sampling算法发表在这篇论文里了。
当我们踌躇于MPI的扩展性不理想而MapReduce的效率不理想时,Google MapReduce团队的几个人分出去,开发了一个新的并行框架Pregel。当时Pregel项目的tech lead访问中国。这个叫Grzegorz Malewicz的波兰人说服了我尝试在Pregel框架下验证LDA。但是在说这个故事之前,我们先看看Google Rephil——另一个基于MapReduce实现的并行隐含语义分析系统。
应st叔叔邀请,打算写一写topic model的知识与大家探讨。Topic model一个典型特点是:难度不大,但涉及的知识相对繁杂。这两天稍加整理后更是加深了这个认识。若作一篇,篇幅太长,各位估计也没读下去的动力;于是计划出一个系列,对每个部分加以梳理,并尽可能使其详整、连贯。
预计目录如下(随时调整):
- 熟悉的频率学派:从pLSA谈起
- MLE
- E-M算法
- 向Bayesian转变:基础理论
- 先验后验 & 共轭分布
- Beta函数, Gamma函数 & Dirichlet分布
- 一门大学问:采样
- Markov chain及其平稳分布
- MCMC & Metropolis-Hastings算法
- Gibbs sampling
- 终于等到你:LDA
- 物理意义
- 模型搭建
- Training & Inference
- Summary & Reference
整个series预计在今年9月完成。不过扛着boss压力,不排除有延期可能(求st叔轻轻拍)。
感谢大家阅读、批判。
首次看本专栏文章的小伙建议先看一下介绍专栏结构的这篇文章:专栏文章分类及各类内容简介。
由于LDA论文所涉及的内容比较多,所以把讲解LDA论文的文章分成4篇子文章,以方便小伙伴们阅读,下面是各个子文章的主要内容及文章链接:
(一)早期文本模型的简介
(二)LDA的建模介绍
(三)用变分推理求解LDA模型的参数
(四)Gensim简介、LDA编程实现、LDA主题提取效果图展示
本篇文章承接上一篇文章“(三)用变分推理求解LDA模型的参数”,来介绍一下Gensim,以及如何利用Gensim编程实现LDA(完整的代码在这里),并展示了LDA主题提取效果图。
本篇是LDA系列文章的最后一篇,主要包含三个部分的内容:(1)介绍Python开源主题模型包Gensim的一些基本使用方法,便于读者快速上手;(2)利用Gensim包,通过若干篇中文新闻训练出一个LDA模型;(3)利用训练出的模型对这些文本信息进行主题提取并可视化提取结果。
Gensim非常适合用来实现各种文本模型、主题模型,包括tf-idf模型、LSI模型以及LDA模型。本节简单介绍一下Gensim中核心的三个数据结构、必须要掌握的一些基础用法,有了这些基本上可以快速编程实现LDA等主题模型。关于Gensim的一些特性,比如内存不依赖性、存储中间结果等本文本介绍了,感兴趣的小伙伴可以去看Gensim的官方文档。
Gensim的用法主要围绕着三个核心的概念而展开:corpus(语料库)、model(模型)、vector(向量)。
假设我们现在有一个语料库,里面包括着9篇文档,每篇文档里面有若干单词:

现在我们要通过Gensim里面的一些API将其数字化,以便后续的计算处理。首先我们引入corpora模块里面的dictionary类,对这个语料库建立字典。在Gensim里面,对语料库建立字典是指把语料库中所有的词语统计好,再分别记录下这些词语在这个语料库中出现的次数,存在一个Python的字典中,如下所示:

之后我们调用dictionary类下面的doc2bow函数,将这个语料库转化为gensim里面 corpus,这是语料库中每篇文档都变成了一个list(从形状上看就是一个vetcor),list的每个元素是一个元组,元组的第一个元素代表词在字典中的编号,第二个元素代表这个词在这篇文档中出现的次数,注意,如果某个词在这篇文档中出现了0次,则不被记录到corpus中,以节省空间,所以这样的list也被称为稀疏向量(sparse vector)。所以这个语料库对应着如下的corpus:

以下是导入语料库、去掉stop word、建立字典、建立corpus对应的代码:
# remove stop words and split each document, then we get texts f = open(‘test-doc.txt’) stop_list = set(‘for a of the and to in’.split()) texts = [[word for word in line.strip().lower().split() if word not in stop_list] for line in f] print(‘Text = ’, texts)
# build the dictionary, a dict of (question, answer) pair dictionary = corpora.Dictionary(texts) print(dictionary.token2id)
# transform the whole texts to vector(sparse) corpus = [dictionary.doc2bow(text) for text in texts] print(corpus)
现在,这个corpus可以认为是“原始的模型(model)”,因为它就是单纯的词的计数统计结果。现在,我们利用model模块下的TfidfModel方法以我们刚建立的corpus作为参数,初始化一个tfidf model,这样我们就得到了一个模型,这个模型可以把任何其他形式的的corpus转化为tfidf形式的corpus,即每个词对应的数值是这个词的tf-idf值,不再是单纯的词频计数了。是不是很方便呢?如果想转化为其他模型,按照同样的方式转化即可,目前,Gensim里面常用的基础文本模型还有LSI模型、LDA模型。将一个原始的模型转化为tf-idf模型的代码如下:
讯享网# create a transformation, from initial model to tf-idf model tfidf = models.TfidfModel(corpus) # step 1 – initialize a model # “tfidf” is treated as a read-only object that can be used to convert any vector from the old representation # (bag-of-words integer counts) to the new representation (TfIdf real-valued weights): doc_bow = [(0, 1), (1, 1)] print(tfidf[doc_bow]) # step 2 – use the model to transform vectors # apply a transformation to a whole corpus corpus_tfidf = tfidf[corpus] for doc in corpus_tfidf:
<span class="k">print</span><span class="p">(</span><span class="n">doc</span><span class="p">)</span></code></pre></div><p data-pid="YJZi3wwg">上述就是gensim包最最基础的几个用法了。下面我们就利用这些方法来实现一下LDA。</p><p class="ztext-empty-paragraph"><br/></p><p class="ztext-empty-paragraph"><br/></p><div class="highlight"><pre><code class="language-python"><span class="k">def</span> <span class="nf">load_stopword</span><span class="p">():</span> <span class="n">f_stop</span> <span class="o">=</span> <span class="nb">open</span><span class="p">(</span><span class="s1">'sw.txt'</span><span class="p">)</span> <span class="n">sw</span> <span class="o">=</span> <span class="p">[</span><span class="n">line</span><span class="o">.</span><span class="n">strip</span><span class="p">()</span> <span class="k">for</span> <span class="n">line</span> <span class="ow">in</span> <span class="n">f_stop</span><span class="p">]</span> <span class="n">f_stop</span><span class="o">.</span><span class="n">close</span><span class="p">()</span> <span class="k">return</span> <span class="n">sw</span> # remove the stop words sw = load_stopword() f = open(‘news_cn.dat’, encoding=‘utf-8’) # load the text data texts = [[word for word in line.strip().lower().split() if word not in sw] for line in f] f.close()
接下来我们对这个语料库建立对应的字典,再把其从原始的corpus转为tf-idf模型corpus(其实直接转成LDA模型的corpus也可以,只是回顾一下上面的知识而已)。然后,我们调用model模块下面的Ldamodel方法将其转化为LDA模型的corpus,调用的时候有几个参数解释一下:

至此,通过我们导入的语料库,一个LDA模型已经训练完成,我们想要的信息都在这个模型里面了。这部分代码如下:
讯享网# build the dictionary for texts dictionary = corpora.Dictionary(texts) dict_len = len(dictionary) # transform the whole texts to sparse vector corpus = [dictionary.doc2bow(text) for text in texts] # create a transformation, from initial model to tf-idf model corpus_tfidf = models.TfidfModel(corpus)[corpus] num_topics = 9 # create a transformation, from tf-idf model to lda model lda = models.LdaModel(corpus_tfidf, num_topics=num_topics, id2word=dictionary,
<span class="n">alpha</span><span class="o">=</span><span class="mf">0.01</span><span class="p">,</span> <span class="n">eta</span><span class="o">=</span><span class="mf">0.01</span><span class="p">,</span> <span class="n">minimum_probability</span><span class="o">=</span><span class="mf">0.001</span><span class="p">,</span> <span class="n">update_every</span> <span class="o">=</span> <span class="mi">1</span><span class="p">,</span> <span class="n">chunksize</span> <span class="o">=</span> <span class="mi">100</span><span class="p">,</span> <span class="n">passes</span> <span class="o">=</span> <span class="mi">1</span><span class="p">)</span></code></pre></div><p class="ztext-empty-paragraph"><br/></p><p data-pid="5Raqx1DM">这个语料库中一共有2043篇文档,我们提取出了9中主题,每个主题我们展示了其概率最大的7个词语以及对应的概率,同时我们输出了前9个文档分别属于这九个主题的概率。</p><p data-pid="iA-VGlSC">首先,我们打印出来了前9个文档分别属于这九个主题的概率,代码如下:</p><div class="highlight"><pre><code class="language-python"><span class="c1"># 打印前9个文档的主题</span> num_show_topic = 9 # 每个文档显示前几个主题 print(‘下面,显示前9个文档的主题分布:’) doc_topics = lda.get_document_topics(corpus_tfidf) # 所有文档的主题分布 for i in range(9):
讯享网<span class="n">topic</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">(</span><span class="n">doc_topics</span><span class="p">[</span><span class="n">i</span><span class="p">])</span> <span class="n">topic_distribute</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">(</span><span class="n">topic</span><span class="p">[:,</span> <span class="mi">1</span><span class="p">])</span> <span class="n">topic_idx</span> <span class="o">=</span> <span class="nb">list</span><span class="p">(</span><span class="n">topic_distribute</span><span class="p">)</span> <span class="k">print</span><span class="p">(</span><span class="s1">'第</span><span class="si">%d</span><span class="s1">个文档的 </span><span class="si">%d</span><span class="s1"> 个主题分布概率分别为:'</span> <span class="o">%</span> <span class="p">(</span><span class="n">i</span><span class="p">,</span> <span class="n">num_show_topic</span><span class="p">))</span> <span class="k">print</span><span class="p">(</span><span class="n">topic_idx</span><span class="p">)</span></code></pre></div><p data-pid="97l6Omps">输出结果如图所示:</p><figure><img src="https://pic2.zhimg.com/v2-3872bdaeb01e07f685ea8594b_r.jpg" data-rawwidth="554" data-rawheight="243" class="origin_image zh-lightbox-thumb" width="554" data-original="https://pic2.zhimg.com/v2-3872bdaeb01e07f685ea8594b_r.jpg"/></figure><p data-pid="AX2e0CC5">接下来,我们打印出每个主题其概率最大的7个词语以及对应的概率,代码如下:</p><div class="highlight"><pre><code class="language-python"><span class="n">num_show_term</span> <span class="o">=</span> <span class="mi">7</span> <span class="c1"># 每个主题下显示几个词</span> for topic_id in range(num_topics):
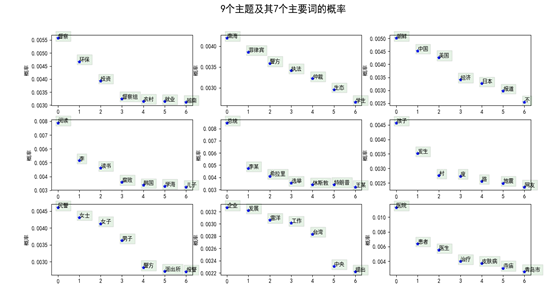
<span class="k">print</span><span class="p">(</span><span class="s1">'第</span><span class="si">%d</span><span class="s1">个主题的词与概率如下:</span><span class="se">\t</span><span class="s1">'</span> <span class="o">%</span> <span class="n">topic_id</span><span class="p">)</span> <span class="n">term_distribute_all</span> <span class="o">=</span> <span class="n">lda</span><span class="o">.</span><span class="n">get_topic_terms</span><span class="p">(</span><span class="n">topicid</span><span class="o">=</span><span class="n">topic_id</span><span class="p">)</span> <span class="n">term_distribute</span> <span class="o">=</span> <span class="n">term_distribute_all</span><span class="p">[:</span><span class="n">num_show_term</span><span class="p">]</span> <span class="n">term_distribute</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">(</span><span class="n">term_distribute</span><span class="p">)</span> <span class="n">term_id</span> <span class="o">=</span> <span class="n">term_distribute</span><span class="p">[:,</span> <span class="mi">0</span><span class="p">]</span><span class="o">.</span><span class="n">astype</span><span class="p">(</span><span class="n">np</span><span class="o">.</span><span class="n">int</span><span class="p">)</span> <span class="k">print</span><span class="p">(</span><span class="s1">'词:</span><span class="se">\t</span><span class="s1">'</span><span class="p">,</span> <span class="n">end</span><span class="o">=</span><span class="s1">' '</span><span class="p">)</span> <span class="k">for</span> <span class="n">t</span> <span class="ow">in</span> <span class="n">term_id</span><span class="p">:</span> <span class="k">print</span><span class="p">(</span><span class="n">dictionary</span><span class="o">.</span><span class="n">id2token</span><span class="p">[</span><span class="n">t</span><span class="p">],</span> <span class="n">end</span><span class="o">=</span><span class="s1">' '</span><span class="p">)</span> <span class="k">print</span><span class="p">(</span><span class="s1">'</span><span class="se">\n</span><span class="s1">概率:</span><span class="se">\t</span><span class="s1">'</span><span class="p">,</span> <span class="n">term_distribute</span><span class="p">[:,</span> <span class="mi">1</span><span class="p">])</span></code></pre></div><p data-pid="IKrdEt3S">输出结果如图所示:</p><figure><img src="https://pic3.zhimg.com/v2-6afc1e2c12f02ddf658_r.jpg" data-rawwidth="554" data-rawheight="336" class="origin_image zh-lightbox-thumb" width="554" data-original="https://pic3.zhimg.com/v2-6afc1e2c12f02ddf658_r.jpg"/></figure><p data-pid="02G371qL">在可视化部分,我们首先画出了九个主题的7个词的概率分布图,代码如下:</p><div class="highlight"><pre><code class="language-python"><span class="n">mpl</span><span class="o">.</span><span class="n">rcParams</span><span class="p">[</span><span class="s1">'font.sans-serif'</span><span class="p">]</span> <span class="o">=</span> <span class="p">[</span><span class="sa">u</span><span class="s1">'SimHei'</span><span class="p">]</span> mpl.rcParams[‘axes.unicode_minus’] = False for i, k in enumerate(range(num_topics)):
讯享网<span class="n">ax</span> <span class="o">=</span> <span class="n">plt</span><span class="o">.</span><span class="n">subplot</span><span class="p">(</span><span class="mi">3</span><span class="p">,</span> <span class="mi">3</span><span class="p">,</span> <span class="n">i</span><span class="o">+</span><span class="mi">1</span><span class="p">)</span> <span class="n">item_dis_all</span> <span class="o">=</span> <span class="n">lda</span><span class="o">.</span><span class="n">get_topic_terms</span><span class="p">(</span><span class="n">topicid</span><span class="o">=</span><span class="n">k</span><span class="p">)</span> <span class="n">item_dis</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">(</span><span class="n">item_dis_all</span><span class="p">[:</span><span class="n">num_show_term</span><span class="p">])</span> <span class="n">ax</span><span class="o">.</span><span class="n">plot</span><span class="p">(</span><span class="nb">range</span><span class="p">(</span><span class="n">num_show_term</span><span class="p">),</span> <span class="n">item_dis</span><span class="p">[:,</span> <span class="mi">1</span><span class="p">],</span> <span class="s1">'b*'</span><span class="p">)</span> <span class="n">item_word_id</span> <span class="o">=</span> <span class="n">item_dis</span><span class="p">[:,</span> <span class="mi">0</span><span class="p">]</span><span class="o">.</span><span class="n">astype</span><span class="p">(</span><span class="n">np</span><span class="o">.</span><span class="n">int</span><span class="p">)</span> <span class="n">word</span> <span class="o">=</span> <span class="p">[</span><span class="n">dictionary</span><span class="o">.</span><span class="n">id2token</span><span class="p">[</span><span class="n">i</span><span class="p">]</span> <span class="k">for</span> <span class="n">i</span> <span class="ow">in</span> <span class="n">item_word_id</span><span class="p">]</span> <span class="n">ax</span><span class="o">.</span><span class="n">set_ylabel</span><span class="p">(</span><span class="sa">u</span><span class="s2">"概率"</span><span class="p">)</span> <span class="k">for</span> <span class="n">j</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="n">num_show_term</span><span class="p">):</span> <span class="n">ax</span><span class="o">.</span><span class="n">text</span><span class="p">(</span><span class="n">j</span><span class="p">,</span> <span class="n">item_dis</span><span class="p">[</span><span class="n">j</span><span class="p">,</span> <span class="mi">1</span><span class="p">],</span> <span class="n">word</span><span class="p">[</span><span class="n">j</span><span class="p">],</span> <span class="n">bbox</span><span class="o">=</span><span class="nb">dict</span><span class="p">(</span><span class="n">facecolor</span><span class="o">=</span><span class="s1">'green'</span><span class="p">,</span><span class="n">alpha</span><span class="o">=</span><span class="mf">0.1</span><span class="p">))</span> plt.suptitle(u‘9个主题及其7个主要词的概率’, fontsize=18) plt.show()
效果图如下所示:
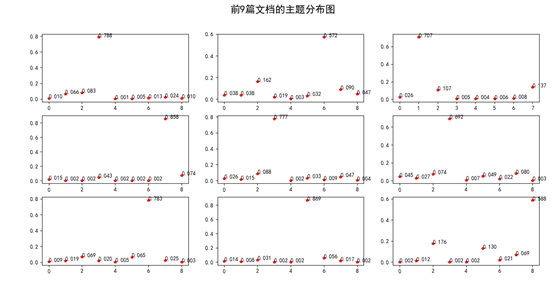
接着我们画出了前9篇文档分别属于这9个主题的概率分布图,代码如下:
for i in range(9):讯享网<span class="n">ax</span> <span class="o">=</span> <span class="n">plt</span><span class="o">.</span><span class="n">subplot</span><span class="p">(</span><span class="mi">3</span><span class="p">,</span> <span class="mi">3</span><span class="p">,</span> <span class="n">i</span> <span class="o">+</span> <span class="mi">1</span><span class="p">)</span> <span class="n">doc_item</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">(</span><span class="n">doc_topics</span><span class="p">[</span><span class="n">i</span><span class="p">])</span> <span class="n">doc_item_id</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">(</span><span class="n">doc_item</span><span class="p">[:,</span> <span class="mi">0</span><span class="p">])</span> <span class="n">doc_item_dis</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">array</span><span class="p">(</span><span class="n">doc_item</span><span class="p">[:,</span> <span class="mi">1</span><span class="p">])</span> <span class="n">ax</span><span class="o">.</span><span class="n">plot</span><span class="p">(</span><span class="n">doc_item_id</span><span class="p">,</span> <span class="n">doc_item_dis</span><span class="p">,</span> <span class="s1">'r*'</span><span class="p">)</span> <span class="k">for</span> <span class="n">j</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="n">doc_item</span><span class="o">.</span><span class="n">shape</span><span class="p">[</span><span class="mi">0</span><span class="p">]):</span> <span class="n">ax</span><span class="o">.</span><span class="n">text</span><span class="p">(</span><span class="n">doc_item_id</span><span class="p">[</span><span class="n">j</span><span class="p">],</span> <span class="n">doc_item_dis</span><span class="p">[</span><span class="n">j</span><span class="p">],</span> <span class="s1">'</span><span class="si">%.3f</span><span class="s1">'</span> <span class="o">%</span> <span class="n">doc_item_dis</span><span class="p">[</span><span class="n">j</span><span class="p">])</span> plt.suptitle(u‘前9篇文档的主题分布图’, fontsize=18) plt.show()
效果图如下所示:
好了,以上就是这篇文章要讲解的三大主要内容了。利用Gensim实现了一个LDA模型后,对LDA应该会有更加直观清晰的认识。
(LDA系列文章(包括(一)、(二)、(三)、(四))的全部参考资料)
- 德菲涅定理维基百科
- Gensim官方文档
- 悉尼科技大学徐亦达老师的讲义
- 悉尼科技大学徐亦达老师的教学视频
- 一篇解析LDA论文中Figure2的博客
- chinahadoop
- 师兄在理解难点处的讲解~
以下内容来自刘建平Pinard-博客园的学习笔记,总结如下:
在前面我们讲到了基于矩阵分解的LSI和NMF主题模型,这里我们开始讨论被广泛使用的主题模型:隐含狄利克雷分布(Latent Dirichlet Allocation,以下简称LDA)。
注意机器学习还有一个LDA,即线性判别分析,主要是用于降维和分类的。
文本关注于隐含狄利克雷分布对应的LDA。
1.1 LDA贝叶斯模型
LDA是基于贝叶斯模型的,涉及到贝叶斯模型离不开“先验分布”,“数据(似然)”和“后验分布”三块。在贝叶斯学派这里:
先验分布 + 数据(似然)= 后验分布
这点其实很好理解,因为这符合我们人的思维方式,比如你对好人和坏人的认知,先验分布为:100个好人和100个的坏人,即你认为好人坏人各占一半,现在你被2个好人(数据)帮助了和1个坏人骗了,于是你得到了新的后验分布为:102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布,当你被1个好人(数据)帮助了和3个坏人(数据)骗了后,你又更新了你的后验分布为:103个好人和104个的坏人。依次继续更新下去。
1.2 二项分布与Beta分布
对于上一节的贝叶斯模型和认知过程,假如用数学和概率的方式该如何表达呢?
对于我们的数据(似然),这个好办,用一个二项分布就可以搞定,即对于二项分布:
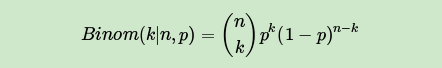
其中p我们可以理解为好人的概率,k为好人的个数,n为好人坏人的总数。
虽然数据(似然)很好理解,但是对于先验分布,我们就要费一番脑筋了,为什么呢?因为我们希望这个先验分布和数据(似然)对应的二项分布集合后,得到的后验分布在后面还可以作为先验分布!就像上面例子里的“102个好人和101个的坏人”,它是前面一次贝叶斯推荐的后验分布,又是后一次贝叶斯推荐的先验分布。也即是说,我们希望先验分布和后验分布的形式应该是一样的,这样的分布我们一般叫共轭分布。在我们的例子里,我们希望找到和二项分布共轭的分布。
和二项分布共轭的分布其实就是Beta分布。Beta分布的表达式为:
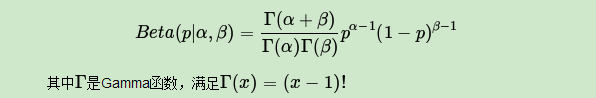
仔细观察Beta分布和二项分布,可以发现两者的密度函数很相似,区别仅仅在前面的归一化的阶乘项。那么它如何做到先验分布和后验分布的形式一样呢?后验分布  推导如下:
推导如下:
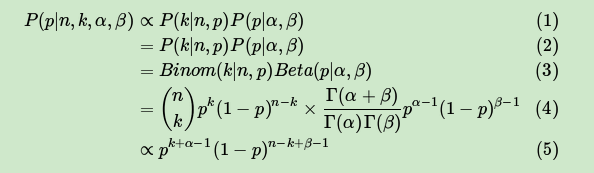
将上面最后的式子归一化以后,得到我们的后验概率为:
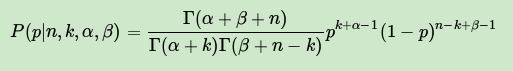
可见后验分布的确是Beta分布,而且我们发现:
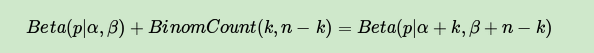
这个式子完全符合我们在上一节好人坏人例子里的情况,我们的认知会把数据里的好人坏人数分别加到我们的先验分布上,得到后验分布。
来看看Beta分布  的期望:
的期望:
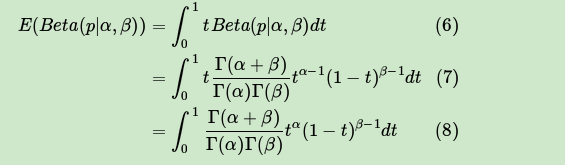
由于上式最右边的乘积对应Beta分布  ,因此有:
,因此有:
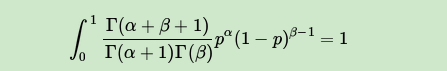
这样我们的期望可以表达为:
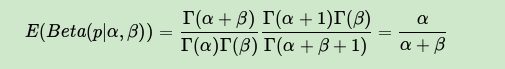
这个结果也很符合我们的思维方式。
1.3 多项分布与Dirichlet 分布
现在我们回到上面好人坏人的问题,假如我们发现有第三类人,不好不坏的人,这时候我们如何用贝叶斯来表达这个模型分布呢?之前我们是二维分布,现在是三维分布。
由于二维我们使用了Beta分布和二项分布来表达这个模型,则在三维时,以此类推,我们可以用三维的Beta分布来表达先验后验分布,三项的多项分布来表达数据(似然)。
三项的多项分布好表达,假设数据中的第一类有  个好人,第二类有
个好人,第二类有  个坏人,第三类为
个坏人,第三类为  个不好不坏的人,对应的概率分别为
个不好不坏的人,对应的概率分别为  ,则对应的多项分布为:
,则对应的多项分布为:
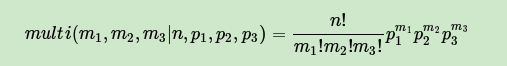
那三维的Beta分布呢?超过二维的Beta分布我们一般称之为狄利克雷(以下称为Dirichlet )分布。
也可以说Beta分布是Dirichlet 分布在二维时的特殊形式。
从二维的Beta分布表达式,我们很容易写出三维的Dirichlet分布如下:
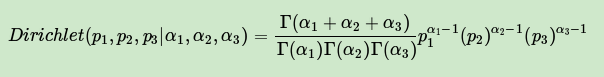
同样的方法,我们可以写出4维,5维以及更高维的Dirichlet 分布的概率密度函数。为了简化表达式,我们用向量来表示概率和计数,这样多项分布可以表示为:
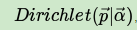
而多项分布可以表示为:
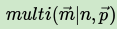
一般意义上的K维Dirichlet 分布表达式为:
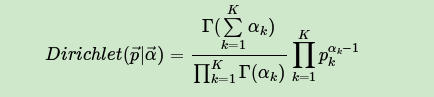
而多项分布和Dirichlet 分布也满足共轭关系,这样可以得到和上一节类似的结论:
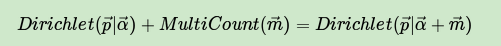
对于Dirichlet 分布的期望,也有和Beta分布类似的性质:
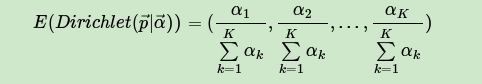
1.4 LDA主题模型
前面做了这么多的铺垫,我们终于可以开始LDA主题模型了。
问题是这样的,我们有  篇文档,对应第
篇文档,对应第  个文档中有
个文档中有  个词。即输入如下图
个词。即输入如下图
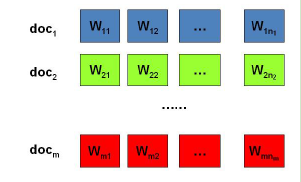
我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。在LDA模型中,我们需要先假定一个主题数目K,这样所有的分布就都基于K个主题展开。那么具体LDA模型是怎么样的呢?具体如下图:
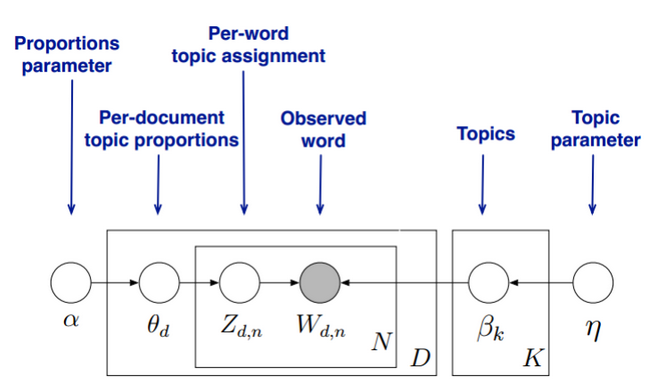
LDA假设文档主题的先验分布是Dirichlet分布,即对于任一文档  ,其主题分布
,其主题分布  为
为
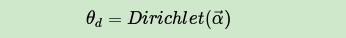
其中,  为分布的超参数,是一个
为分布的超参数,是一个  维向量。
维向量。
LDA假设主题中词的先验分布是Dirichlet分布,即对于任一主题  ,其词分布
,其词分布  为
为
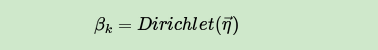
其中,  为分布的超参数,是一个
为分布的超参数,是一个  维向量。
维向量。  代表词汇表里所有词的个数。
代表词汇表里所有词的个数。
对于数据中任一一篇文档  中的第
中的第  个词,可以从主题分布
个词,可以从主题分布  中得到它的主题编号
中得到它的主题编号  的分布为:
的分布为:

而对于该主题编号,得到我们看到的词  的概率分布为:
的概率分布为:
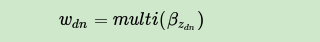
理解LDA主题模型的主要任务就是理解上面的这个模型。
这个模型里,我们有  个文档主题的Dirichlet分布,而对应的数据有
个文档主题的Dirichlet分布,而对应的数据有  个主题编号的多项分布 ,这样
个主题编号的多项分布 ,这样  就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。
就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。
如果在第d个文档中,第k个主题的词的个数为:  ,则对应的多项分布的计数可以表示为
,则对应的多项分布的计数可以表示为
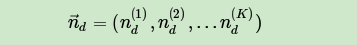
利用Dirichlet-multi共轭,得到  的后验分布为:
的后验分布为:
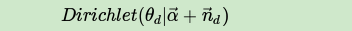
同样的道理,对于主题与词的分布,我们有K个主题与词的Dirichlet分布,而对应的数据有K个主题编号的多项分布,这样  就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。
就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。
如果在第k个主题中,第v个词的个数为:  ,则对应的多项分布的计数可以表示为
,则对应的多项分布的计数可以表示为
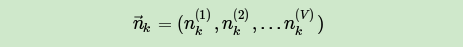
利用Dirichlet-multi共轭,得到  的后验分布为:
的后验分布为:
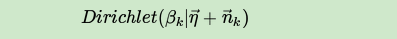
由于主题产生词不依赖具体某一个文档,因此文档主题分布和主题词分布是独立的。理解了上面这M+K组Dirichlet-multi共轭,就理解了LDA的基本原理了。
现在的问题是,基于这个LDA模型如何求解我们想要的每一篇文档的主题分布和每一个主题中词的分布呢?
一般有两种方法,第一种是基于Gibbs采样算法求解,第二种是基于变分推断EM算法求解。
2.1 Gibbs采样算法求解LDA的思路
首先,回顾LDA的模型图如下:
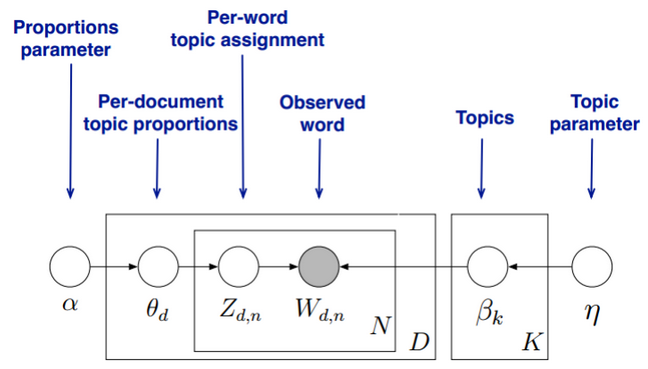
在Gibbs采样算法求解LDA的方法中,α,η是已知的先验输入,我们的目标是得到各个  对应的整体
对应的整体  的概率分布,即文档主题的分布和主题词的分布。由于我们是采用Gibbs采样法,则对于要求的目标分布,我们需要得到对应分布各个特征维度的条件概率分布。
的概率分布,即文档主题的分布和主题词的分布。由于我们是采用Gibbs采样法,则对于要求的目标分布,我们需要得到对应分布各个特征维度的条件概率分布。
具体到我们的问题,所有文档联合起来形成的词向量w是已知的数据,不知道的是语料库主题
z的分布。假如我们可以先求出w,z的联合分布  ,进而可以求出某一个词
,进而可以求出某一个词  对应主题特征
对应主题特征  的条件概率分布
的条件概率分布  ,其中
,其中  代表去掉下标为
代表去掉下标为  的词后的主题分布。有了条件概率分布
的词后的主题分布。有了条件概率分布  ,就可以进行Gibbs采样,最终在Gibbs采样收敛后得到第i个词的主题。
,就可以进行Gibbs采样,最终在Gibbs采样收敛后得到第i个词的主题。
如果我们通过采样得到了所有词的主题,那么通过统计所有词的主题计数,就可以得到各个主题的词分布。接着统计各个文档对应词的主题计数,就可以得到各个文档的主题分布。
以上就是Gibbs采样算法求解LDA的思路。
2.2 主题和词的联合分布与条件分布的求解
从上一节可以发现,要使用Gibbs采样求解LDA,关键是得到条件概率  的表达式。这一节我们的目标就是求出这个表达式供Gibbs采样使用。
的表达式。这一节我们的目标就是求出这个表达式供Gibbs采样使用。
首先简化下Dirichlet分布的表达式,其中  是归一化参数:
是归一化参数:
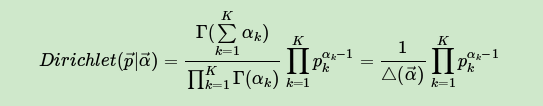
现在先计算下第d个文档的主题的条件分布  ,由于
,由于  组成了Dirichlet-multi共轭,利用这组分布,计算
组成了Dirichlet-multi共轭,利用这组分布,计算  如下:
如下:
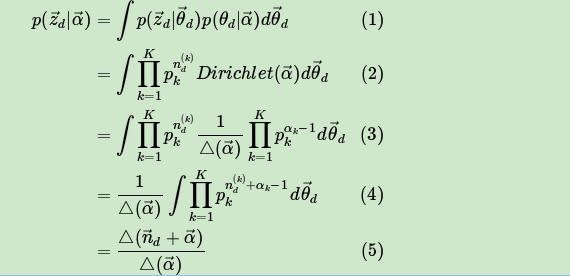
其中,在第d个文档中,第k个主题的词的个数表示为:  ,对应的多项分布的计数可以表示为
,对应的多项分布的计数可以表示为
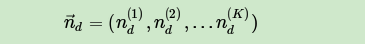
有了单个文档的主题条件分布,则可以得到所有文档的主题条件分布为:
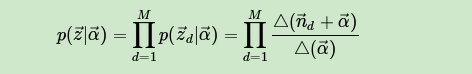
同样的方法,可以得到,第k个主题对应的词的条件分布  为:
为:
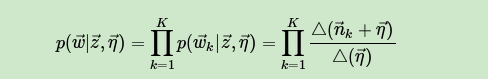
其中,第k个主题中,第v个词的个数表示为:  ,对应的多项分布的计数可以表示为
,对应的多项分布的计数可以表示为
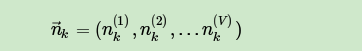
最终我们得到主题和词的联合分布  如下:
如下:
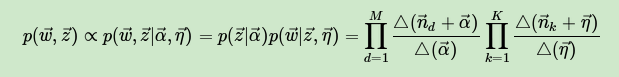
有了联合分布,现在我们就可以求Gibbs采样需要的条件分布  了。需要注意的是这里的i是一个二维下标,对应第d篇文档的第n个词。
了。需要注意的是这里的i是一个二维下标,对应第d篇文档的第n个词。
对于下标  ,由于它对应的词
,由于它对应的词  是可以观察到的,因此有:
是可以观察到的,因此有:
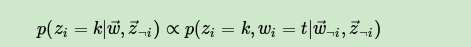
对于  ,它只涉及到第d篇文档和第k个主题两个Dirichlet-multi共轭,即:
,它只涉及到第d篇文档和第k个主题两个Dirichlet-multi共轭,即:
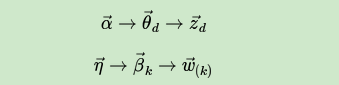
其余的M+K−2个Dirichlet-multi共轭和它们这两个共轭是独立的。如果我们在语料库中去掉  ,并不会改变之前的M+K个Dirichlet-multi共轭结构,只是向量的某些位置的计数会减少,因此对于
,并不会改变之前的M+K个Dirichlet-multi共轭结构,只是向量的某些位置的计数会减少,因此对于  ,对应的后验分布为:
,对应的后验分布为:
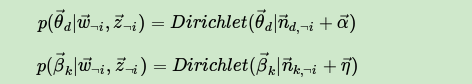
现在开始计算Gibbs采样需要的条件概率:
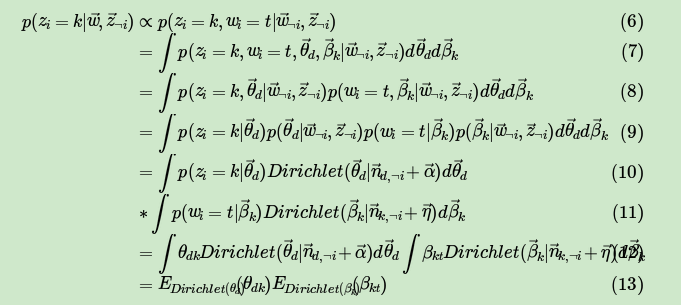
因此我们有:
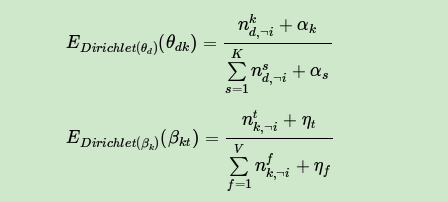
最终我们得到每个词对应主题的Gibbs采样的条件概率公式为:
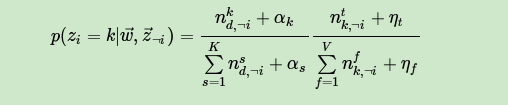
有了这个公式,我们就可以用Gibbs采样去采样所有词的主题,当Gibbs采样收敛后,即得到所有词的采样主题。
利用所有采样得到的词和主题的对应关系,我们就可以得到每个文档词主题的分布  和每个主题中所有词的分布
和每个主题中所有词的分布  。
。
2.3 LDA Gibbs采样算法流程总结
现在我们总结下LDA Gibbs采样算法流程。首先是训练流程:
1) 选择合适的主题数K, 选择合适的超参数向量α,η
2) 对应语料库中每一篇文档的每一个词,随机的赋予一个主题编号z
3) 重新扫描语料库,对于每一个词,利用Gibbs采样公式更新它的topic编号,并更新语料库中该词的编号。
4) 重复第2步的基于坐标轴轮换的Gibbs采样,直到Gibbs采样收敛。
5) 统计语料库中的各个文档各个词的主题,得到文档主题分布  ,统计语料库中各个主题词的分布,得到LDA的主题与词的分布
,统计语料库中各个主题词的分布,得到LDA的主题与词的分布  。
。
下面我们再来看看当新文档出现时,如何统计该文档的主题。
此时我们的模型已定,也就是LDA的各个主题的词分布  已经确定,我们需要得到的是该文档的主题分布。因此在Gibbs采样时,我们的
已经确定,我们需要得到的是该文档的主题分布。因此在Gibbs采样时,我们的  已经固定,只需要对前半部分
已经固定,只需要对前半部分  进行采样计算即可。
进行采样计算即可。
现在我们总结下LDA Gibbs采样算法的预测流程:
1) 对应当前文档的每一个词,随机的赋予一个主题编号z。
2) 重新扫描当前文档,对于每一个词,利用Gibbs采样公式更新它的topic编号。
3) 重复第2步的基于坐标轴轮换的Gibbs采样,直到Gibbs采样收敛。
4) 统计文档中各个词的主题,得到该文档主题分布。
2.4 LDA Gibbs采样算法小结
使用Gibbs采样算法训练LDA模型,我们需要先确定三个超参数K,α,η。
其中选择一个合适的K尤其关键,这个值一般和我们解决问题的目的有关。如果只是简单的语义区分,则较小的K即可,如果是复杂的语义区分,则K需要较大,而且还需要足够的语料。
由于Gibbs采样可以很容易的并行化,因此也可以很方便的使用大数据平台来分布式的训练海量文档的LDA模型。以上就是LDA Gibbs采样算法。
LDA的变分推断EM算法求解,应用于Spark MLlib和Scikit-learn的LDA算法实现,因此值得好好理解。
3.1 变分推断EM算法求解LDA的思路
首先,回顾LDA的模型图如下:
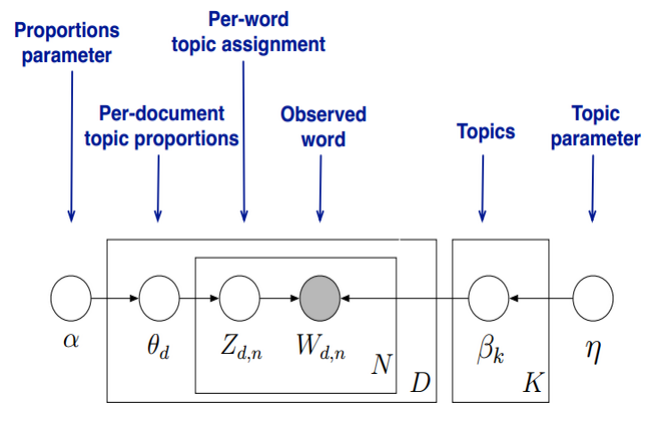
变分推断EM算法希望通过“变分推断(Variational Inference)”和EM算法来得到LDA模型的文档主题分布和主题词分布。
首先来看EM算法在这里的使用,我们的模型里面有隐藏变量θ,β,z,模型的参数是α,η。为了求出模型参数和对应的隐藏变量分布,EM算法需要在E步先求出隐藏变量θ,β,z的基于条件概率分布的期望,接着在M步极大化这个期望,得到更新的后验模型参数α,η。
问题是在EM算法的E步,由于θ,β,z的耦合,我们难以求出隐藏变量θ,β,z的条件概率分布,也难以求出对应的期望,需要“变分推断“来帮忙,这里所谓的变分推断,也就是在隐藏变量存在耦合的情况下,我们通过变分假设,即假设所有的隐藏变量都是通过各自的独立分布形成的,这样就去掉了隐藏变量之间的耦合关系。我们用各个独立分布形成的变分分布来模拟近似隐藏变量的条件分布,这样就可以顺利的使用EM算法了。
当进行若干轮的E步和M步的迭代更新之后,我们可以得到合适的近似隐藏变量分布θ,β,z和模型后验参数α,η,进而就得到了我们需要的LDA文档主题分布和主题词分布。
可见要完全理解LDA的变分推断EM算法,需要搞清楚它在E步变分推断的过程和推断完毕后EM算法的过程。
3.2 LDA的变分推断思路
要使用EM算法,我们需要求出隐藏变量的条件概率分布如下:
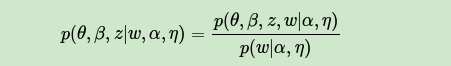
前面讲到由于θ,β,z之间的耦合,这个条件概率是没法直接求的,但是如果不求它就不能用EM算法了。怎么办呢,我们引入变分推断,具体是引入基于mean field assumption的变分推断,这个推断假设所有的隐藏变量都是通过各自的独立分布形成的,如下图所示:
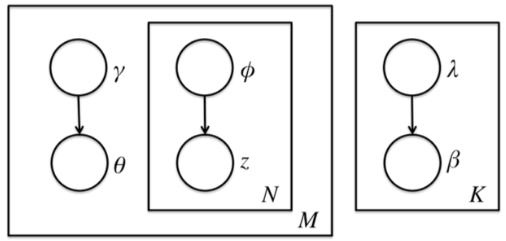
我们假设隐藏变量θ是由独立分布γ形成的,隐藏变量z是由独立分布ϕ形成的,隐藏变量
β是由独立分布λ形成的。这样我们得到了三个隐藏变量联合的变分分布q为:
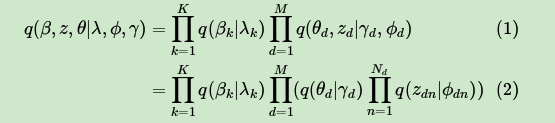
目标是用  来近似的估计
来近似的估计  ,也就是说需要这两个分布尽可能的相似,用数学语言来描述就是希望这两个概率分布之间有尽可能小的KL距离,即:
,也就是说需要这两个分布尽可能的相似,用数学语言来描述就是希望这两个概率分布之间有尽可能小的KL距离,即:
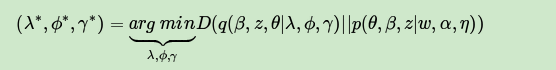
其中  即为
即为  散度或
散度或  距离,对应分布
距离,对应分布  和
和  的交叉熵。即:
的交叉熵。即:
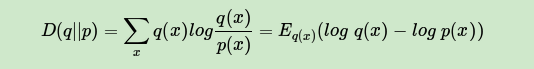
我们的目的就是找到合适的  ,然后用
,然后用  来近似隐藏变量的条件分布
来近似隐藏变量的条件分布  ,进而使用EM算法迭代。
,进而使用EM算法迭代。
先看看文档数据的对数似然函数  如下,为了简化表示,用
如下,为了简化表示,用  代替
代替  ,用来表示
,用来表示  对于变分分布
对于变分分布  的期望。
的期望。
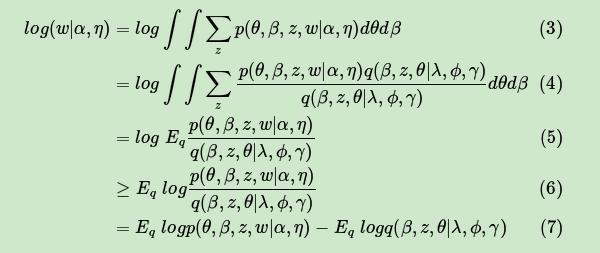
其中,从第(5)式到第(6)式用到了Jensen不等式:
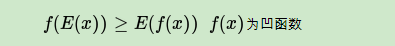
一般把第(7)式记为:
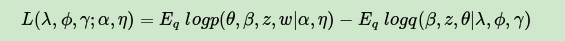
由于  是我们的对数似然的一个下界(第6式),所以这个L一般称为ELBO(Evidence Lower BOund)。那么这个ELBO和我们需要优化的的KL散度有什么关系呢?注意到:
是我们的对数似然的一个下界(第6式),所以这个L一般称为ELBO(Evidence Lower BOund)。那么这个ELBO和我们需要优化的的KL散度有什么关系呢?注意到:
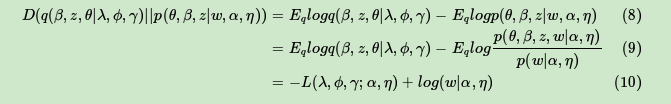
在(10)式中,由于对数似然部分和我们的KL散度无关,可以看做常量,因此我们希望最小化KL散度等价于最大化ELBO。那么我们的变分推断最终等价的转化为要求ELBO的最大值。现在我们开始关注于极大化ELBO并求出极值对应的变分参数λ,ϕ,γ。
3.3 极大化ELBO求解变分参数
为了极大化ELBO,我们首先对ELBO函数做一个整理如下:
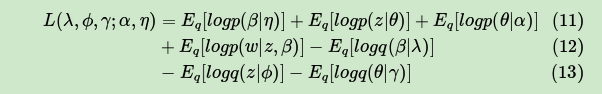
可见展开后有7项,现在我们需要对这7项分别做一个展开。为了简化篇幅,这里只对第一项的展开做详细介绍。在介绍第一项的展开前,我们需要了解指数分布族的性质。指数分布族是指下面这样的概率分布:
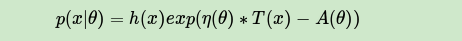
其中,A(x)为归一化因子,主要是保证概率分布累积求和后为1,引入指数分布族主要是它有下面这样的性质:
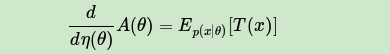
这个证明并不复杂,这里不累述。我们的常见分布比如Gamma分布,Beta分布,Dirichlet分布都是指数分布族。有了这个性质,意味着我们在ELBO里面一大推的期望表达式可以转化为求导来完成,这个技巧大大简化了计算量。
回到我们ELBO第一项的展开如下:
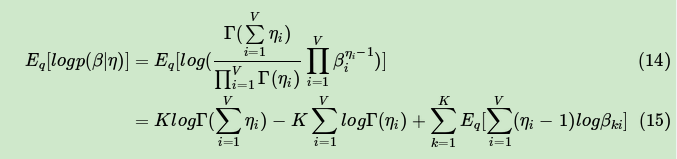
第(15)式的第三项的期望部分,可以用上面讲到的指数分布族的性质,转化为一个求导过程。即:
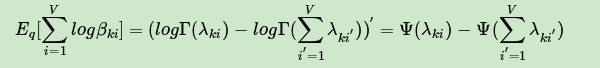
其中:
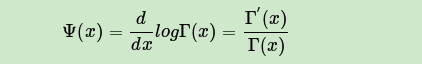
最终,我们得到EBLO第一项的展开式为:
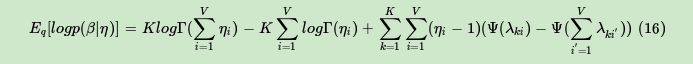
类似的方法求解其他6项,可以得到ELBO的最终关于变分参数λ,ϕ,γ的表达式。其他6项的表达式为:
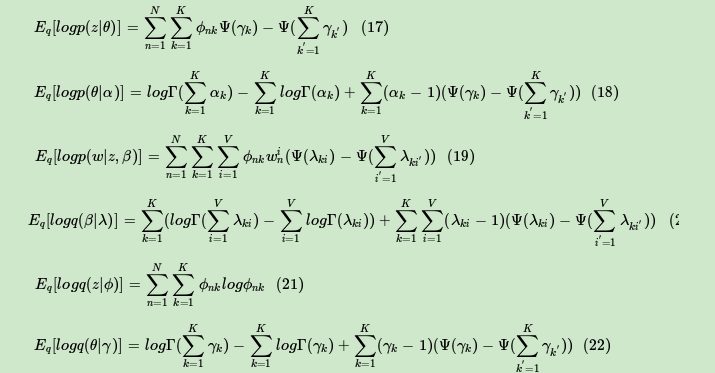
有了ELBO的具体的关于变分参数λ,ϕ,γ的表达式,我们就可以用EM算法来迭代更新变分参数和模型参数了。
3.4 EM算法之E步:获取最优变分参数
有了前面变分推断得到的ELBO函数为基础,我们就可以进行EM算法了。但是和EM算法不同的是这里的E步需要在包含期望的EBLO计算**的变分参数。
如何求解**的变分参数呢?通过对ELBO函数对各个变分参数λ,ϕ,γ分别求导并令偏导数为0,可以得到迭代表达式,多次迭代收敛后即为**变分参数。
这里就不详细推导了,直接给出各个变分参数的表达式如下:

最终我们的E步就是用(23)(24)(26)式来更新三个变分参数。当我们得到三个变分参数后,不断循环迭代更新,直到这三个变分参数收敛。当变分参数收敛后,下一步就是M步,固定变分参数,更新模型参数α,η了。
3.5 EM算法之M步:更新模型参数
由于我们在E步,已经得到了当前**变分参数,现在我们在M步就来固定变分参数,极大化ELBO得到最优的模型参数α,η。求解最优的模型参数α,η的方法有很多,梯度下降法,牛顿法都可以。LDA这里一般使用的是牛顿法,即通过求出ELBO对于α,η的一阶导数和二阶导数的表达式,然后迭代求解α,η在M步的最优解。
对于α,它的一阶导数和二阶导数的表达式为:
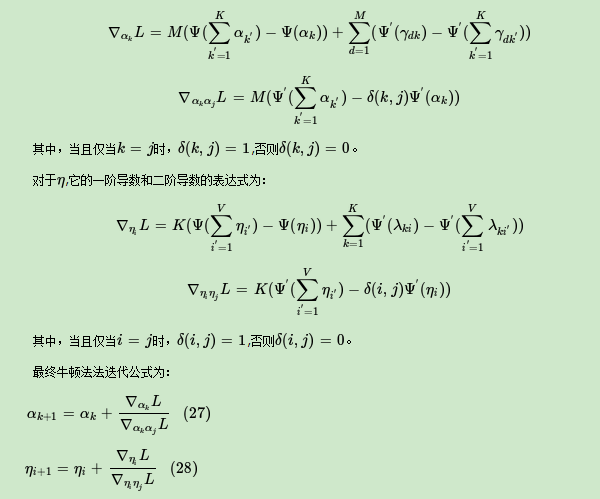
3.6 LDA变分推断EM算法流程总结
下面总结下LDA变分推断EM的算法的概要流程。
输入:主题数K,M个文档与对应的词。

算法结束后,我们可以得到模型的后验参数α,η,以及我们需要的近似模型主题词分布λ,以及近似训练文档主题分布γ。
从应用的角度来使用scikit-learn来学习LDA主题模型。
除了scikit-learn, 还有spark MLlib和gensim库也有LDA主题模型的类库,使用的原理基本类似,本文关注于scikit-learn中LDA主题模型的使用。
4.1 scikit-learn LDA主题模型概述
在scikit-learn中,LDA主题模型的类在sklearn.decomposition.LatentDirichletAllocation包中,其算法实现主要基于变分推断EM算法,而没有使用基于Gibbs采样的MCMC算法实现。
而具体到变分推断EM算法,scikit-learn除了我们原理篇里讲到的标准的变分推断EM算法外,还实现了另一种在线变分推断EM算法,它在原理篇里的变分推断EM算法的基础上,为了避免文档内容太多太大而超过内存大小,而提供了分步训练(partial_fit函数),即一次训练一小批样本文档,逐步更新模型,最终得到所有文档LDA模型的方法。
4.2 scikit-learn LDA主题模型主要参数和方法
我们来看看LatentDirichletAllocation类的主要输入参数:
1) n_topics: 即我们的隐含主题数K,需要调参。K的大小取决于我们对主题划分的需求,比如我们只需要类似区分是动物,植物,还是非生物这样的粗粒度需求,那么K值可以取的很小,个位数即可。如果我们的目标是类似区分不同的动物以及不同的植物,不同的非生物这样的细粒度需求,则K值需要取的很大,比如上千上万。此时要求我们的训练文档数量要非常的多。
2) doc_topicprior:即我们的文档主题先验Dirichlet分布  https://www.zhihu.com/equation?tex=%5Ctheta%7Bd%7D” alt=“\theta_{d}” eeimg=“1”/> 的参数α。一般如果我们没有主题分布的先验知识,可以使用默认值1/K。
https://www.zhihu.com/equation?tex=%5Ctheta%7Bd%7D” alt=“\theta_{d}” eeimg=“1”/> 的参数α。一般如果我们没有主题分布的先验知识,可以使用默认值1/K。
3) topic_wordprior:即我们的主题词先验Dirichlet分布  https://www.zhihu.com/equation?tex=%5Cbeta%7Bk%7D” alt=“\beta_{k}” eeimg=“1”/> 的参数η。一般如果我们没有主题分布的先验知识,可以使用默认值1/K。
https://www.zhihu.com/equation?tex=%5Cbeta%7Bk%7D” alt=“\beta_{k}” eeimg=“1”/> 的参数η。一般如果我们没有主题分布的先验知识,可以使用默认值1/K。
4) learning_method: 即LDA的求解算法。有 ‘batch’ 和 ‘online’两种选择。 ‘batch’即我们在原理篇讲的变分推断EM算法,而“online”即在线变分推断EM算法,在“batch”的基础上引入了分步训练,将训练样本分批,逐步一批批的用样本更新主题词分布的算法。默认是“online”。选择了‘online’则我们可以在训练时使用partial_fit函数分布训练。不过在scikit-learn 0.20版本中默认算法会改回到“batch”。建议样本量不大只是用来学习的话用“batch”比较好,这样可以少很多参数要调。而样本太多太大的话,“online”则是首先了。
5)learning_decay:仅仅在算法使用“online”时有意义,取值最好在(0.5, 1.0],以保证 “online”算法渐进的收敛。主要控制“online”算法的学习率,默认是0.7。一般不用修改这个参数。
6)learning_offset:仅仅在算法使用“online”时有意义,取值要大于1。用来减小前面训练样本批次对最终模型的影响。
7) max_iter :EM算法的最大迭代次数。
8)total_samples:仅仅在算法使用“online”时有意义, 即分步训练时每一批文档样本的数量。在使用partial_fit函数时需要。
9)batch_size: 仅仅在算法使用“online”时有意义, 即每次EM算法迭代时使用的文档样本的数量。
10)mean_change_tol :即E步更新变分参数的阈值,所有变分参数更新小于阈值则E步结束,转入M步。一般不用修改默认值。
11) max_doc_update_iter: 即E步更新变分参数的最大迭代次数,如果E步迭代次数达到阈值,则转入M步。
从上面可以看出,如果learning_method使用“batch”算法,则需要注意的参数较少,则如果使用“online”,则需要注意“learning_decay”, “learning_offset”,“total_samples”和“batch_size”等参数。无论是“batch”还是“online”, n_topics(K), doc_topic_prior(α), topic_word_prior(η)都要注意。如果没有先验知识,则主要关注与主题数K。可以说,主题数K是LDA主题模型最重要的超参数。
4.3 scikit-learn LDA中文主题模型实例
下面我们给一个LDA中文主题模型的简单实例,从分词一直到LDA主题模型。
我们的有下面三段文档语料,分别放在了nlp_test0.txt, nlp_test2.txt和 nlp_test4.txt:沙瑞金赞叹易学习的胸怀,是金山的百姓有福,可是这件事对李达康的触动很大。易学习又回忆起他们三人分开的前一晚,大家一起喝酒话别,易学习被降职到道口县当县长,王大路下海经商,李达康连连赔礼道歉,觉得对不起大家,他最对不起的是王大路,就和易学习一起给王大路凑了5万块钱,王大路自己东挪西撮了5万块,开始下海经商。没想到后来王大路竟然做得风生水起。沙瑞金觉得他们三人,在困难时期还能以沫相助,很不容易。 沙瑞金向毛娅打听他们家在京州的别墅,毛娅笑着说,王大路事业有成之后,要给欧阳菁和她公司的股权,她们没有要,王大路就在京州帝豪园买了三套别墅,可是李达康和易学习都不要,这些房子都在王大路的名下,欧阳菁好像去住过,毛娅不想去,她觉得房子太大很浪费,自己家住得就很踏实。 347年(永和三年)三月,桓温兵至彭模(今四川彭山东南),留下参军周楚、孙盛看守辎重,自己亲率步兵直攻成都。同月,成汉将领李福袭击彭模,结果被孙盛等人击退;而桓温三战三胜,一直逼近成都。首先我们进行分词,并把分词结果分别存在nlp_test1.txt, nlp_test3.txt和 nlp_test5.txt:


现在我们读入分好词的数据到内存备用,并打印分词结果观察:

打印出的分词结果如下:
讯享网沙瑞金 赞叹 易学习 的 胸怀 , 是 金山 的 百姓 有福 , 可是 这件 事对 李达康 的 触动 很大 。 易学习 又 回忆起 他们 三人 分开 的 前一晚 , 大家 一起 喝酒 话别 , 易学习 被 降职 到 道口 县当 县长 , 王大路 下海经商 , 李达康 连连 赔礼道歉 , 觉得 对不起 大家 , 他 最 对不起 的 是 王大路 , 就 和 易学习 一起 给 王大路 凑 了 5 万块 钱 , 王大路 自己 东挪西撮 了 5 万块 , 开始 下海经商 。 没想到 后来 王大路 竟然 做 得 风生水 起 。 沙瑞金 觉得 他们 三人 , 在 困难 时期 还 能 以沫 相助 , 很 不 容易 。 沙瑞金 向 毛娅 打听 他们 家 在 京州 的 别墅 , 毛娅 笑 着 说 , 王大路 事业有成 之后 , 要 给 欧阳 菁 和 她 公司 的 股权 , 她们 没有 要 , 王大路 就 在 京州 帝豪园 买 了 三套 别墅 , 可是 李达康 和 易学习 都 不要 , 这些 房子 都 在 王大路 的 名下 , 欧阳 菁 好像 去 住 过 , 毛娅 不想 去 , 她 觉得 房子 太大 很 浪费 , 自己 家住 得 就 很 踏实 。 347 年 ( 永和 三年 ) 三月 , 桓温 兵至 彭模 ( 今 四川 彭山 东南 ) , 留下 参军 周楚 、 孙盛 看守 辎重 , 自己 亲率 步兵 直攻 成都 。 同月 , 成汉 将领 李福 袭击 彭模 , 结果 被 孙盛 等 人 击退 ; 而 桓温 三 战三胜 , 一直 逼近 成都 。
我们接着导入停用词表。

接着我们要把词转化为词频向量,注意由于LDA是基于词频统计的,因此一般不用TF-IDF来做文档特征。代码如下:
输出即为所有文档中各个词的词频向量。有了这个词频向量,我们就可以来做LDA主题模型了,由于我们只有三个文档,所以选择主题数K=2。代码如下:

通过fit_transform函数,我们就可以得到文档的主题模型分布在docres中。而主题词 分布则在lda.components_中。我们将其打印出来:

文档主题的分布如下:
[[ 0.00 0.] [ 0.0 0. ] [ 0. 0.0]]可见第一个和第二个文档较大概率属于主题2,则第三个文档属于主题1.
主题和词的分布如下:
讯享网[[ 1. 1. 0. 0. 0. 0. 1. 1. 0. 0. 0. 1. 0. 0. 1.00 0. 1.0 1.
在实际的应用中,我们需要对K,α,η进行调参。如果是“online”算法,则可能需要对“online”算法的一些参数做调整。这里只是给出了LDA主题模型从原始文档到实际LDA处理的过程。
1.1. 先来瞎扯扯
上期的方差分析说到了它的发明者英国大统计学家R.A.Fisher,期间我们说到周志华的西瓜书里提及的Fisher判别分析仍是这个大统计学家Fisher提出的,并且Fisher 判别分析中用到了方差分析的思想,这一期我们就来较为详细地聊一聊Fisher判别分析。(Fisher判别分析,Fisher Discriminant Analysis,或称线性判别分析,Linear Discriminant Analysis,简称LDA。这里特别说明,下文也参考到了周志华的西瓜书。)
1.2. 好人?坏人?
说到判别两字,我们从小就在用。小时候看影视作品时,总是会试着去“判别”某一个人是好人还是坏人。现在我们回归童年,想想看我们以前是怎么区分好人坏人的。之前看一些影视作品的时候,可能会将好人归为做了好事的一类,坏人归为做了坏事的一类;也可能觉得某个人和好人很接近,关系很好,所以这个人也是好人;或者是某个人很痛恨坏人,打击罪犯,除暴安良,那么这个人也是好人。
把我们的童年记忆留住,想想看怎么教计算机去进行判别分析吧!
1.3. 模式识别系统的基本构成
判别分析隶属于模式识别这个大的学科中,模式识别系统的基本构成有数据采集,特征选取,模式选择,训练测试,计算结果和复杂度分析,进一步反馈。模式识别的具体操作的流程图利用Visio画图如下所示。
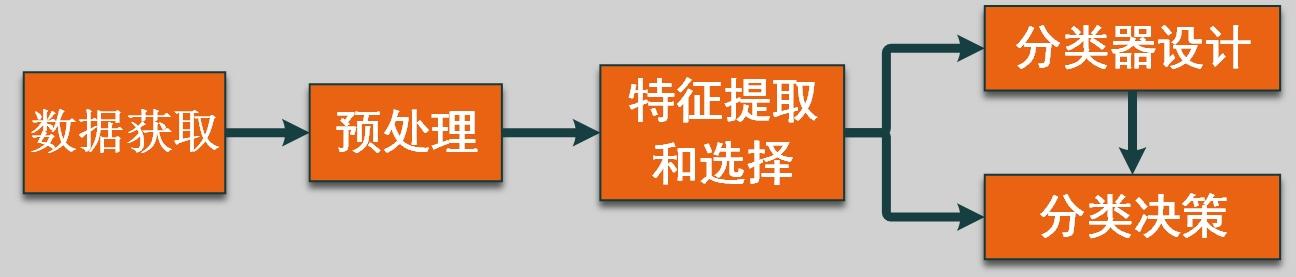
很显然我们今天要用的Fisher判别分析在分类器设计和分类决策里面。
已知研究对象被分成若干类型,并已有一批样本的观测数据,在此基础上根据某些准则建立判别式,然后对未知类型的样本进行判别分类,此即判别分析。
1.4. 简单的判别分析:距离判别法
我们先来看一个最简单的判别分析的方法,距离判别法。
距离判别法首先根据已知分类的数据,分别计算出各类的重心。再根据新个体到每类的距离(即新个体与各类重心的距离,可采用欧氏距离或者马氏距离等等),根据最短的距离确定分类情况。
设有两个总体(两类)  和
和  ,从第一个总体
,从第一个总体  中抽取出
中抽取出  个样本,从第二个总体
个样本,从第二个总体  中抽取出
中抽取出  个样本,每个样本测量p个指标特征。
个样本,每个样本测量p个指标特征。

现今任取一个样本X,实测其p个指标特征的值。  ,问此样品X应被判归为哪一类?
,问此样品X应被判归为哪一类?
首先计算X到  ,
,  总体的距离,分别为
总体的距离,分别为  ,
,  。
。
若采用欧氏距离计算,则有: 
其中  ;
;  表示第i类的重心(也就是均值),
表示第i类的重心(也就是均值),  表示第i类第k个指标的重心。
表示第i类第k个指标的重心。
若采用马氏距离计算,则有

其中  ;
;  表示第i类的重心,
表示第i类的重心,  表示第i类的协方差矩阵的逆矩阵。
表示第i类的协方差矩阵的逆矩阵。

1.5. 判别花瓣种类
距离判别法是利用重心,和哪类的重心隔得更近,就判别为哪一类。而Fisher 判别法则是利用“同类差别较小、不同类差别较大”的原则构造出判别式,再按照判别式的值来判断新个体的类别。
这里我们结合一个识别花瓣种类的实例,结合说明Fisher判别分析(MATLAB 里的判别分析里的例子)。

假设有一个传送带,每次都传一个花瓣过来,这个花瓣肯定是属于三个种类之一的,即Setosa,Versicolor和Virginica中的一个。这些花翻译过来并不通俗,就用A类花瓣,B类花瓣和C类花瓣代替它们好了。现在一个花瓣朝某个工人而来,他需要给这个花瓣打上其种类的标签。传送带一直不间断地传着花瓣过来,这个工人累的不行,贴标签的动作也成了习惯,他感觉自己根本就是《摩登时代》里的卓别林扮演的螺丝工。

他很不开心,大骂,都2018年了,为什么还要做这么简单机械的事情。他便把传送带停下,回去花了些成本安装了一个光学传感器,令其返回每个花瓣的长度,宽度等其他指标。然后写了个Fisher判别分析的程序,根据花瓣的长度和宽度来判别花瓣的种类,就可以获得90%以上的识别成功率。
这里先给出Fisher判别分析的步骤,如果不想了解其原理,而只是想去应用的人,可以根据下面的步骤,不需要看下面的详解(当然还是推荐看原理详解)。
1. 把来自2类的训练样本集划分为2个子集  和
和  ;
;
2. 计算各类的均值向量  ,
,  ;
;  ;
;
3. 计算各类的类内离散矩阵  ,
,  ;
;  ;
;
4. 计算类内总离散矩阵  ;
;
5. 计算矩阵  的逆矩阵
的逆矩阵  ;
;
6. 求出向量  (此处采用拉格朗日乘子法解出Fisher线性判别的**投影方向);
(此处采用拉格朗日乘子法解出Fisher线性判别的**投影方向);
7. 判别函数为  ;
;
8. 判别函数的阈值  可采用以下两种方法确定:第一种是
可采用以下两种方法确定:第一种是  ;第二种是
;第二种是  ;
;
9. 分类规则:比较  值与阈值
值与阈值  的大小,得出其分类。
的大小,得出其分类。
3.1. Matlab实现
首先调用obj=fitcdiscr(X,y)训练模型,其中obj为获得的大量参数的包裹,X 为数据集合,其中行表示样本,列表示指标特征,y为对应的样本的类别。再调用r=predict(obj,Z)来进行预测,r为获得的预测判别结果,Z为需要判别的矩阵(类似于X)。
需要深究,可参看MATLAB的fitcdiscr函数和Discriminant Analysis的help文档画出分割直线。
3.2. 花瓣实例
上面花瓣的实例来自于MATLAB的判别分析的帮助文档,可直接利用上面所述的命令实现花瓣的判别分析。将Fisher线性判别先用在B类花瓣和C类花瓣上,得到判别直线1,后用在A类花瓣和B类花瓣上,得到判别直线2。
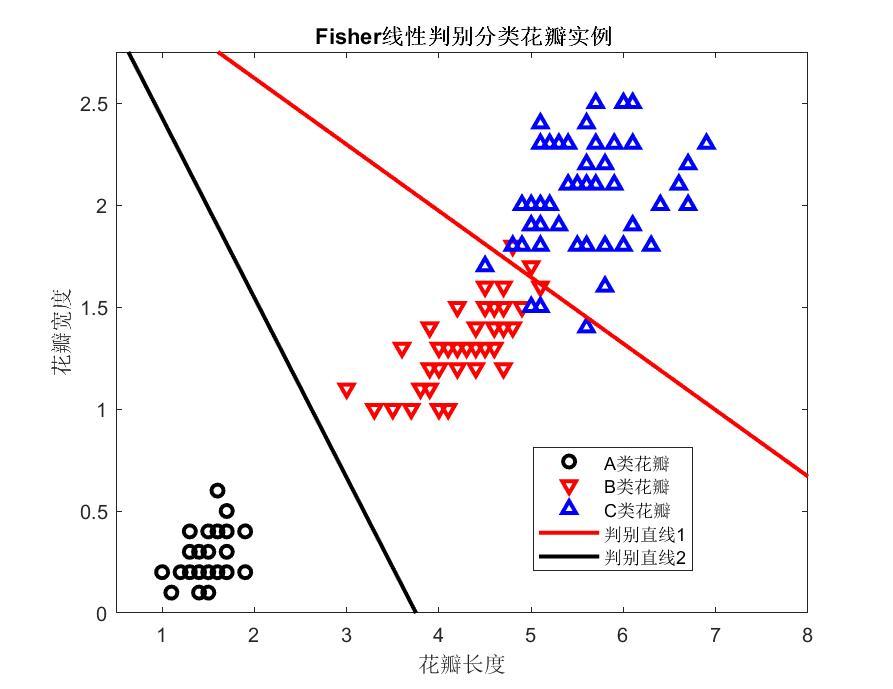
下面我们就来看看Fisher判别分析的详解。
下面的Fisher判别分析是针对2分类问题,对于上面的多分类问题可以采用一些办法进行推广。
4.1. 投影降维
Fisher判别分析的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近、不同类样例的投影点尽可能远离。在对新样本进行分类时,将其投影到同样的这条直线上,再根据新样本投影点的位置来确定它的类别。如下所示,给出了一个二维示意图。
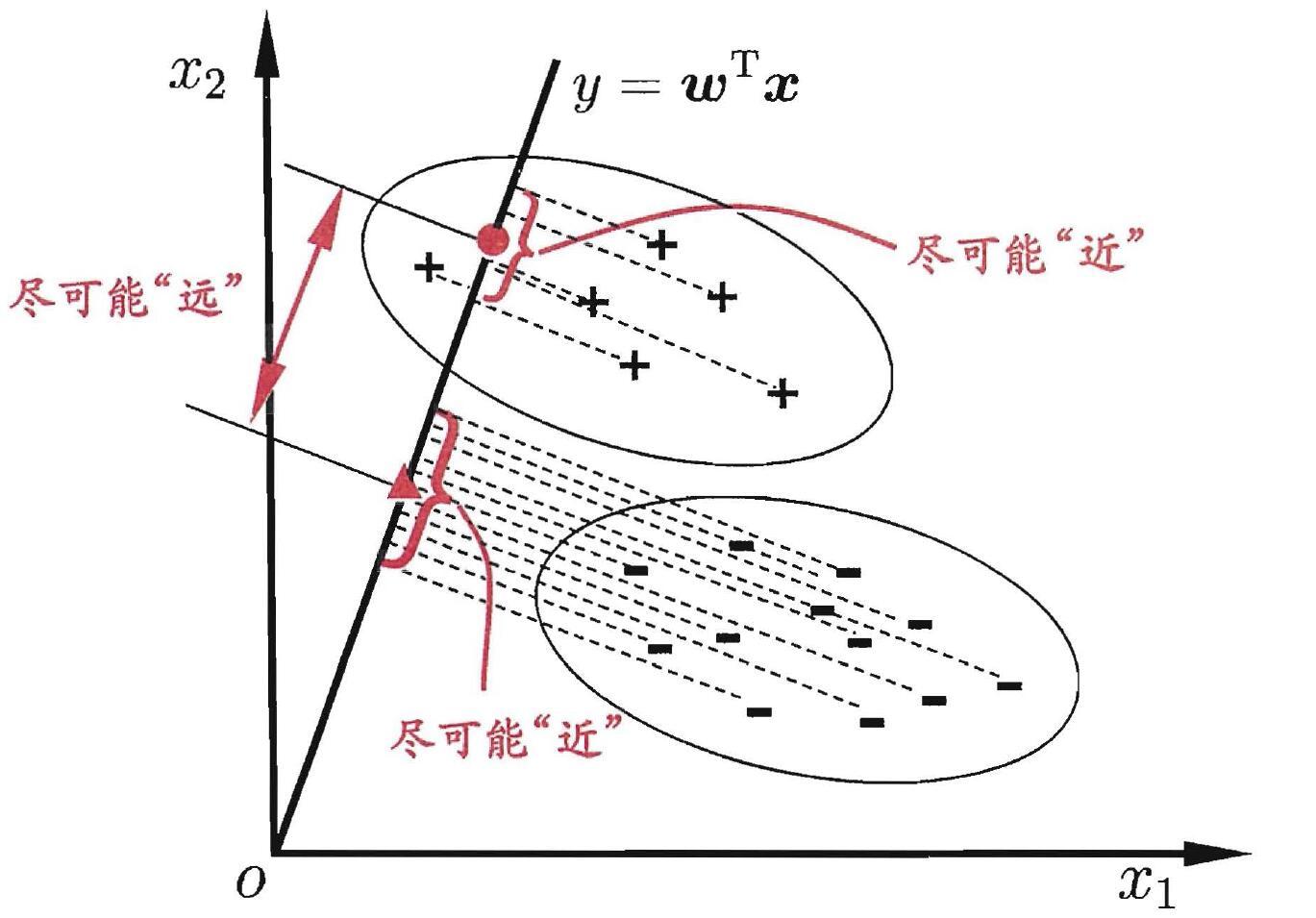
上面二维示意图中的“+”、“-”分别代表正例和反例,椭圆表示数据簇的外轮廓,虚线表示投影,红色实心圆和红色实心三角形分别表示两类样本投影后的中心点。给定数据集  ,
,  ,令
,令  、
、  分别表示第
分别表示第  类示例的集合、均值向量。若将数据投影到直线
类示例的集合、均值向量。若将数据投影到直线  上,则两类样本的中心在直线上的投影分别为
上,则两类样本的中心在直线上的投影分别为  和
和  。
。
上面这张图来自于周志华的西瓜书,这里我稍加解释下几个问题。
1:为什么画过原点?
答:我们所关心的仅仅是这些点到一条直线投下来的影子点之间的距离,所以直线可以沿着投影方向随意平移,这并不影响它的影子点之间的距离。因此直线经过垂直方向平移后,肯定可以过原点。
2:怎么理解  ?
?
答:w在这里可以理解为这条过原点直线的单位方向向量。而  ,可以直接利用向量的内积去几何形象地理解它。
,可以直接利用向量的内积去几何形象地理解它。 
其中  为两个向量的夹角。因此通过
为两个向量的夹角。因此通过  变换,所有的点都转换为这条直线上的点,得到的值为与原点的距离(原点的一侧为正,另一侧为负)。
变换,所有的点都转换为这条直线上的点,得到的值为与原点的距离(原点的一侧为正,另一侧为负)。
这里我们先回想一下,上一期的方差分析里面的内容。衡量同类样例的投影点的距离尽可能接近,是不是可以考虑方差分析里的组内偏差  呢?而衡量不同类样例的投影点的距离尽可能远,是不是可以考虑到方差分析里的组间偏差
呢?而衡量不同类样例的投影点的距离尽可能远,是不是可以考虑到方差分析里的组间偏差  呢?事实上它们就是一样的。
呢?事实上它们就是一样的。
4.2. 组内偏差
先来看看如何使得同类样例的投影点之间的距离尽可能接近。按照方差分析里的思想,应该把各组内的偏差相加,再把各组的偏差总和相加。
上面我们已经知道  得到的值是
得到的值是  点投影到该直线上的点与原点的距离(带正负的)。现在不妨设
点投影到该直线上的点与原点的距离(带正负的)。现在不妨设  是第0类的,那么
是第0类的,那么  的组内偏差为
的组内偏差为  ,则第0类的组内偏差相加为
,则第0类的组内偏差相加为  。
。
现在我们将上面换个矩阵的写法, 
把  矩阵抽出来,这是个2 阶方阵。
矩阵抽出来,这是个2 阶方阵。
将组内的偏差相加得到式子  ,其形式即为协方差的形式(缺少分母),即两个特征之间(横坐标和纵坐标)的协方差矩阵,记为
,其形式即为协方差的形式(缺少分母),即两个特征之间(横坐标和纵坐标)的协方差矩阵,记为  ,表示第0类示例的协方差矩阵。同样的,记
,表示第0类示例的协方差矩阵。同样的,记  为第1 类示例的协方差矩阵。
为第1 类示例的协方差矩阵。
定义“类内散度矩阵”为  ,则两组的组内偏差总和(最后得到的是一个数)为
,则两组的组内偏差总和(最后得到的是一个数)为 
通过上面的解释,知道使得同类样例的投影点之间的距离尽可能接近,只需使得  最小化。
最小化。
4.3. 组间偏差
再来看看如何使得不同类样例的投影点之间的距离尽可能远离。按照方差分析里的思想,应该把各组和总体均值的偏差加权相加(这个体现在Fisher的多分类推广里面)。
第0类和第1类的组间偏差为两类的均值到直线上的投影的距离,即
现在我们将上面换个矩阵的写法, 
把  矩阵抽出来,这是个2 阶方阵,定义其为“类间散度矩阵”,即
矩阵抽出来,这是个2 阶方阵,定义其为“类间散度矩阵”,即  ,则两组的组间偏差为
,则两组的组间偏差为  。(最后得到的是一个数。)
。(最后得到的是一个数。)
通过上面的解释,知道使得不同类样例的投影点之间的距离尽可能远离,只需使得  最大化。
最大化。
4.4. **投影
由上,我们需要将同类样例的投影点之间的距离尽可能接近,即最小化  ,不同类样例的投影点之间的距离尽可能远离,即最大化
,不同类样例的投影点之间的距离尽可能远离,即最大化  。
。
构造代价函数 
这就是Fisher线性判别欲最大化的目标,即  和
和  的“广义瑞利商”,从而找到**投影方向
的“广义瑞利商”,从而找到**投影方向  。
。
观察代价函数  ,它只与直线
,它只与直线  的方向有关(与其长度无关,
的方向有关(与其长度无关,  和
和  的
的  值一样),不妨令
值一样),不妨令  ,则最大化代价函数
,则最大化代价函数  也就等价于
也就等价于

采用拉格朗日乘子法,即有  。 对其求导。(这里有关矩阵求导的部分可参看知乎上的矩阵求导术的文章:矩阵求导术)
。 对其求导。(这里有关矩阵求导的部分可参看知乎上的矩阵求导术的文章:矩阵求导术)

其间运用到了标量的转置和  ,
,  为对称阵,根据矩阵求导的法则有
为对称阵,根据矩阵求导的法则有 
令其为0,得到  ,此即直线
,此即直线  为矩阵
为矩阵  的特征向量。
的特征向量。
利用  的式子代入,
的式子代入, 
我们在乎的只是直线  的投影方向,而与长度无关,所以可以将标量
的投影方向,而与长度无关,所以可以将标量  和标量
和标量  甩掉,即得
甩掉,即得  。
。
求逆时,考虑到数值稳定性,在实践中通常是对  进行奇异值分解,即
进行奇异值分解,即  。这里
。这里  是一个实对角矩阵,其对角线上的元素是
是一个实对角矩阵,其对角线上的元素是  的奇异值,然后再由
的奇异值,然后再由  得到
得到  。
。
这样即可计算得到直线  ,和
,和  的垂直的两类的中心线可作为两类的判别直线。
的垂直的两类的中心线可作为两类的判别直线。
4.5. 推广至多分类
假定存在N个类,且第i类的样本数为  。我们先主义“全局散度矩阵”:
。我们先主义“全局散度矩阵”: 
其中  是所有示例的均值向量。
是所有示例的均值向量。
将类内散度矩阵  重定义为每个类别的散度矩阵之和,即
重定义为每个类别的散度矩阵之和,即  ,其中
,其中 
由上知 :
这些和方差分析其实是一一对应的。
显然,多分类LDA可以有多种实现方法:使用  三者中的任何两个即可。常见的一种实现是采用优化目标:
三者中的任何两个即可。常见的一种实现是采用优化目标:

其中  是
是  维的矩阵,
维的矩阵,  表示指标特征的维数,
表示指标特征的维数,  表示矩阵的迹。
表示矩阵的迹。
上式可通过广义特征值问题求解: 
 的闭式解则是
的闭式解则是  的
的  个最大广义特征值所对应的特征向量组成的矩阵。
个最大广义特征值所对应的特征向量组成的矩阵。
若将  视为一个投影矩阵,则多分类LDA将样本投影到
视为一个投影矩阵,则多分类LDA将样本投影到  维空间,
维空间,  通常远小子数据原有的属性数。于是,可通过这个投影来减小样本点的维数,且投影过程中使用了类别信息,因此LDA也常被视为一种经典的监督降维技术。
通常远小子数据原有的属性数。于是,可通过这个投影来减小样本点的维数,且投影过程中使用了类别信息,因此LDA也常被视为一种经典的监督降维技术。
Fisher判别分析就讲到这里,更多相关的内容推荐参看NG的课程以及周志华的书,这里也推荐他人的两篇NG课程的笔记博客给大家参考:线性判别分析(Linear Discriminant Analysis)(一),线性判别分析(Linear Discriminant Analysis)(二)。
Fisher判别分析,利用投影技术进行降维,降维后计算组内偏差(此处可类比到方差分析中的随机误差),同时计算组间偏差(此处可类比方差分析中的各个因素水平之间的组间偏差),利用凸优化方法找到使得组内偏差最小化、组间偏差最大化的直线或者超平面来分割不同的类别。
声明:转载需联系本人。
LDA可以分为以下5个步骤:
- 一个函数:gamma函数。
- 四个分布:二项分布、多项分布、beta分布、Dirichlet分布。
- 一个概念和一个理念:共轭先验和贝叶斯框架。
- 两个模型:pLSA、LDA。
- 一个采样:Gibbs采样
关于LDA有两种含义,一种是线性判别分析(Linear Discriminant Analysis),一种是概率主题模型:隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),本文讲后者。
按照wiki上的介绍,LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出,是一种主题模型,它可以将文档集 中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。此外,一篇文档可以包含多个主题,文档中每一个词都由其中的一个主题生成。
人类是怎么生成文档的呢?首先先列出几个主题,然后以一定的概率选择主题,以一定的概率选择这个主题包含的词汇,最终组合成一篇文章。如下图所示(其中不同颜色的词语分别对应上图中不同主题下的词)。

那么LDA就是跟这个反过来:根据给定的一篇文档,反推其主题分布。
在LDA模型中,一篇文档生成的方式如下:
- 从狄利克雷分布
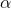
中取样生成文档 i 的主题分布
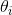
。
- 从主题的多项式分布
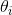
中取样生成文档i第 j 个词的主题
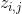
。
- 从狄利克雷分布
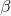
中取样生成主题
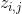
对应的词语分布
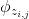
。
- 从词语的多项式分布
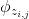
中采样最终生成词语
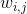
。
其中,类似Beta分布是二项式分布的共轭先验概率分布,而狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布。此外,LDA的图模型结构如下图所示(类似贝叶斯网络结构):
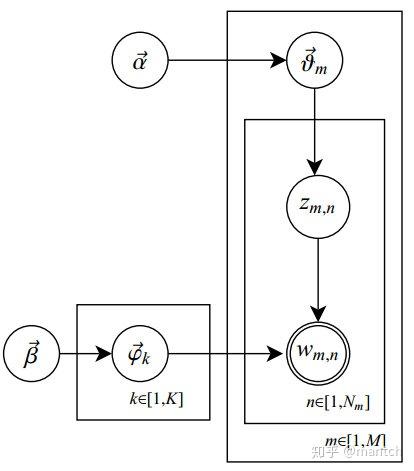
先解释一下以上出现的概念。
- 二项分布(Binomial distribution)
二项分布是从伯努利分布推进的。伯努利分布,又称两点分布或0-1分布,是一个离散型的随机分布,其中的随机变量只有两类取值,非正即负{+,-}。而二项分布即重复n次的伯努利试验,记为
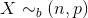
。简言之,只做一次实验,是伯努利分布,重复做了n次,是二项分布。
- 多项分布
是二项分布扩展到多维的情况。多项分布是指单次试验中的随机变量的取值不再是0-1的,而是有多种离散值可能(1,2,3…,k)。比如投掷6个面的骰子实验,N次实验结果服从K=6的多项分布。其中:
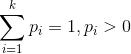
- 共轭先验分布
在贝叶斯统计中,如果后验分布与先验分布属于同类,则先验分布与后验分布被称为共轭分布,而先验分布被称为似然函数的共轭先验。 - Beta分布
二项分布的共轭先验分布。给定参数
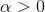
和
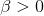
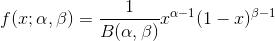
其中:
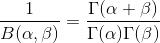
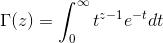
注:这便是所谓的gamma函数,下文会具体阐述。
- 狄利克雷分布
是beta分布在高维度上的推广。Dirichlet分布的的密度函数形式跟beta分布的密度函数如出一辙:
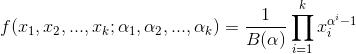
其中
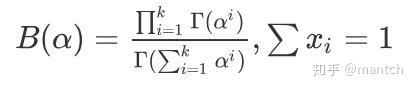
至此,我们可以看到二项分布和多项分布很相似,Beta分布和Dirichlet 分布很相似。
如果想要深究其原理可以参考:通俗理解LDA主题模型,也可以先往下走,最后在回过头来看详细的公式,就更能明白了。
总之,可以得到以下几点信息。
- beta分布是二项式分布的共轭先验概率分布:对于非负实数
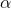
和
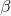
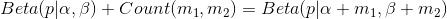
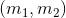
对应的是二项分布
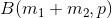
的记数。针对于这种观测到的数据符合二项分布,参数的先验分布和后验分布都是Beta分布的情况,就是Beta-Binomial 共轭。”
- 狄利克雷分布(Dirichlet分布)是多项式分布的共轭先验概率分布,一般表达式如下:
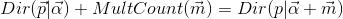
- 贝叶斯派思考问题的固定模式:
先验分布
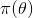
+ 样本信息
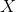
= 后验分布
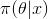
。
在讲LDA模型之前,再循序渐进理解基础模型:Unigram model、mixture of unigrams model,以及跟LDA最为接近的pLSA模型。为了方便描述,首先定义一些变量:
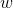
表示词,

示所有单词的个数(固定值)。

表示主题,
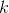
主题的个数(预先给定,固定值)。
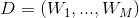
表示语料库,其中的M是语料库中的文档数(固定值)。
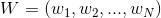
表示文档,其中的N表示一个文档中的词数(随机变量)。
- Unigram model
对于文档
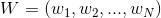
,用
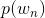
表示词
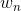
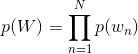
- Mixture of unigrams model
该模型的生成过程是:给某个文档先选择一个主题z,再根据该主题生成文档,该文档中的所有词都来自一个主题。假设主题有
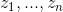
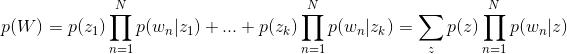
- PLSA模型
理解了pLSA模型后,到LDA模型也就一步之遥——给pLSA加上贝叶斯框架,便是LDA。
在上面的Mixture of unigrams model中,我们假定一篇文档只有一个主题生成,可实际中,一篇文章往往有多个主题,只是这多个主题各自在文档中出现的概率大小不一样。比如介绍一个国家的文档中,往往会分别从教育、经济、交通等多个主题进行介绍。那么在pLSA中,文档是怎样被生成的呢?
假定你一共有K个可选的主题,有V个可选的词,咱们来玩一个扔骰子的游戏。
一、假设你每写一篇文档会制作一颗K面的“文档-主题”骰子(扔此骰子能得到K个主题中的任意一个),和K个V面的“主题-词项” 骰子(每个骰子对应一个主题,K个骰子对应之前的K个主题,且骰子的每一面对应要选择的词项,V个面对应着V个可选的词)。
比如可令K=3,即制作1个含有3个主题的“文档-主题”骰子,这3个主题可以是:教育、经济、交通。然后令V = 3,制作3个有着3面的“主题-词项”骰子,其中,教育主题骰子的3个面上的词可以是:大学、老师、课程,经济主题骰子的3个面上的词可以是:市场、企业、金融,交通主题骰子的3个面上的词可以是:高铁、汽车、飞机。
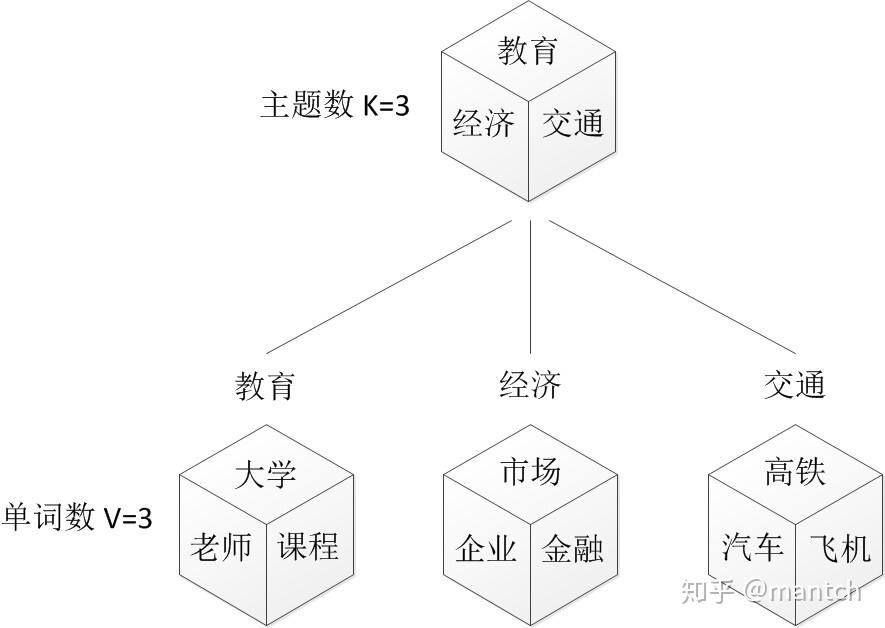
二、每写一个词,先扔该“文档-主题”骰子选择主题,得到主题的结果后,使用和主题结果对应的那颗“主题-词项”骰子,扔该骰子选择要写的词。
先扔“文档-主题”的骰子,假设(以一定的概率)得到的主题是教育,所以下一步便是扔教育主题筛子,(以一定的概率)得到教育主题筛子对应的某个词:大学。
上面这个投骰子产生词的过程简化下便是:“先以一定的概率选取主题,再以一定的概率选取词”。
三、最后,你不停的重复扔“文档-主题”骰子和”主题-词项“骰子,重复N次(产生N个词),完成一篇文档,重复这产生一篇文档的方法M次,则完成M篇文档。
上述过程抽象出来即是PLSA的文档生成模型。在这个过程中,我们并未关注词和词之间的出现顺序,所以pLSA是一种词袋方法。生成文档的整个过程便是选定文档生成主题,确定主题生成词。
反过来,既然文档已经产生,那么如何根据已经产生好的文档反推其主题呢?这个利用看到的文档推断其隐藏的主题(分布)的过程(其实也就是产生文档的逆过程),便是主题建模的目的:自动地发现文档集中的主题(分布)。
文档d和词w是我们得到的样本,可观测得到,所以对于任意一篇文档,其
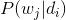
是已知的。从而可以根据大量已知的文档-词项信息
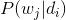
,训练出文档-主题
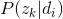
和主题-词项
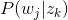
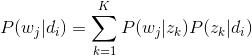
故得到文档中每个词的生成概率为:
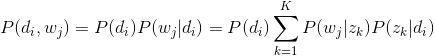
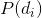
可事先计算求出,而
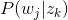
和
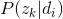
未知,所以
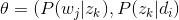
)就是我们要估计的参数(值),通俗点说,就是要最大化这个θ。
用什么方法进行估计呢,常用的参数估计方法有极大似然估计MLE、最大后验证估计MAP、贝叶斯估计等等。因为该待估计的参数中含有隐变量z,所以我们可以考虑EM算法。详细的EM算法可以参考之前写过的 EM算法 章节。
事实上,理解了pLSA模型,也就差不多快理解了LDA模型,因为LDA就是在pLSA的基础上加层贝叶斯框架,即LDA就是pLSA的贝叶斯版本(正因为LDA被贝叶斯化了,所以才需要考虑历史先验知识,才加的两个先验参数)。
下面,咱们对比下本文开头所述的LDA模型中一篇文档生成的方式是怎样的:
- 按照先验概率
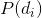
选择一篇文档
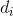
。
- 从狄利克雷分布(即Dirichlet分布)
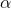
中取样生成文档
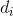
的主题分布
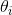
,换言之,主题分布
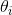
由超参数为
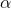
的Dirichlet分布生成。
- 从主题的多项式分布
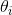
中取样生成文档
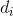
第 j 个词的主题
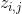
。
- 从狄利克雷分布(即Dirichlet分布)
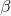
中取样生成主题
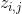
对应的词语分布
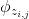
,换言之,词语分布
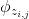
由参数为
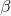
的Dirichlet分布生成。
- 从词语的多项式分布
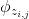
中采样最终生成词语
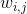
。
LDA中,选主题和选词依然都是两个随机的过程,依然可能是先从主题分布{教育:0.5,经济:0.3,交通:0.2}中抽取出主题:教育,然后再从该主题对应的词分布{大学:0.5,老师:0.3,课程:0.2}中抽取出词:大学。
那PLSA跟LDA的区别在于什么地方呢?区别就在于:
PLSA中,主题分布和词分布是唯一确定的,能明确的指出主题分布可能就是{教育:0.5,经济:0.3,交通:0.2},词分布可能就是{大学:0.5,老师:0.3,课程:0.2}。 但在LDA中,主题分布和词分布不再唯一确定不变,即无法确切给出。例如主题分布可能是{教育:0.5,经济:0.3,交通:0.2},也可能是{教育:0.6,经济:0.2,交通:0.2},到底是哪个我们不再确定(即不知道),因为它是随机的可变化的。但再怎么变化,也依然服从一定的分布,即主题分布跟词分布由Dirichlet先验随机确定。正因为LDA是PLSA的贝叶斯版本,所以主题分布跟词分布本身由先验知识随机给定。
换言之,LDA在pLSA的基础上给这两参数
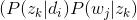
)加了两个先验分布的参数(贝叶斯化):一个主题分布的先验分布Dirichlet分布
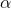
,和一个词语分布的先验分布Dirichlet分布
。
综上,LDA真的只是pLSA的贝叶斯版本,文档生成后,两者都要根据文档去推断其主题分布和词语分布(即两者本质都是为了估计给定文档生成主题,给定主题生成词语的概率),只是用的参数推断方法不同,在pLSA中用极大似然估计的思想去推断两未知的固定参数,而LDA则把这两参数弄成随机变量,且加入dirichlet先验。
所以,pLSA跟LDA的本质区别就在于它们去估计未知参数所采用的思想不同,前者用的是频率派思想,后者用的是贝叶斯派思想。
LDA参数估计:Gibbs采样,详见文末的参考文献。
- 基于经验 主观判断、不断调试、操作性强、最为常用。
- 基于困惑度(主要是比较两个模型之间的好坏)。
- 使用Log-边际似然函数的方法,这种方法也挺常用的。
- 非参数方法:Teh提出的基于狄利克雷过程的HDP法。
- 基于主题之间的相似度:计算主题向量之间的余弦距离,KL距离等。
推荐系统中的冷启动问题是指在没有大量用户数据的情况下如何给用户进行个性化推荐,目的是最优化点击率、转化率或用户 体验(用户停留时间、留存率等)。冷启动问题一般分为用户冷启动、物品冷启动和系统冷启动三大类。
- 用户冷启动是指对一个之前没有行为或行为极少的新用户进行推荐;
- 物品冷启动是指为一个新上市的商品或电影(这时没有与之相关的 评分或用户行为数据)寻找到具有潜在兴趣的用户;
- 系统冷启动是指如何为一个 新开发的网站设计个性化推荐系统。
解决冷启动问题的方法一般是基于内容的推荐。以Hulu的场景为例,对于用 户冷启动来说,我们希望根据用户的注册信息(如:年龄、性别、爱好等)、搜 索关键词或者合法站外得到的其他信息(例如用户使用Facebook账号登录,并得 到授权,可以得到Facebook中的朋友关系和评论内容)来推测用户的兴趣主题。 得到用户的兴趣主题之后,我们就可以找到与该用户兴趣主题相同的其他用户, 通过他们的历史行为来预测用户感兴趣的电影是什么。
同样地,对于物品冷启动问题,我们也可以根据电影的导演、演员、类别、关键词等信息推测该电影所属于的主题,然后基于主题向量找到相似的电影,并将新电影推荐给以往喜欢看这 些相似电影的用户。可以使用主题模型(pLSA、LDA等)得到用户和电影的主题。
以用户为例,我们将每个用户看作主题模型中的一篇文档,用户对应的特征 作为文档中的单词,这样每个用户可以表示成一袋子特征的形式。通过主题模型 学习之后,经常共同出现的特征将会对应同一个主题,同时每个用户也会相应地 得到一个主题分布。每个电影的主题分布也可以用类似的方法得到。
那么如何解决系统冷启动问题呢?首先可以得到每个用户和电影对应的主题向量,除此之外,还需要知道用户主题和电影主题之间的偏好程度,也就是哪些主题的用户可能喜欢哪些主题的电影。当系统中没有任何数据时,我们需要一些先验知识来指定,并且由于主题的数目通常比较小,随着系统的上线,收集到少量的数据之后我们就可以对主题之间的偏好程度得到一个比较准确的估计。
通俗理解LDA主题模型
NLP-LOVE/ML-NLP【机器学习通俗易懂系列文章】
作者: @mantchs
GitHub: https://github.com/NLP-LOVE/ML-NLP
欢迎大家加入讨论!共同完善此项目!群号:【】

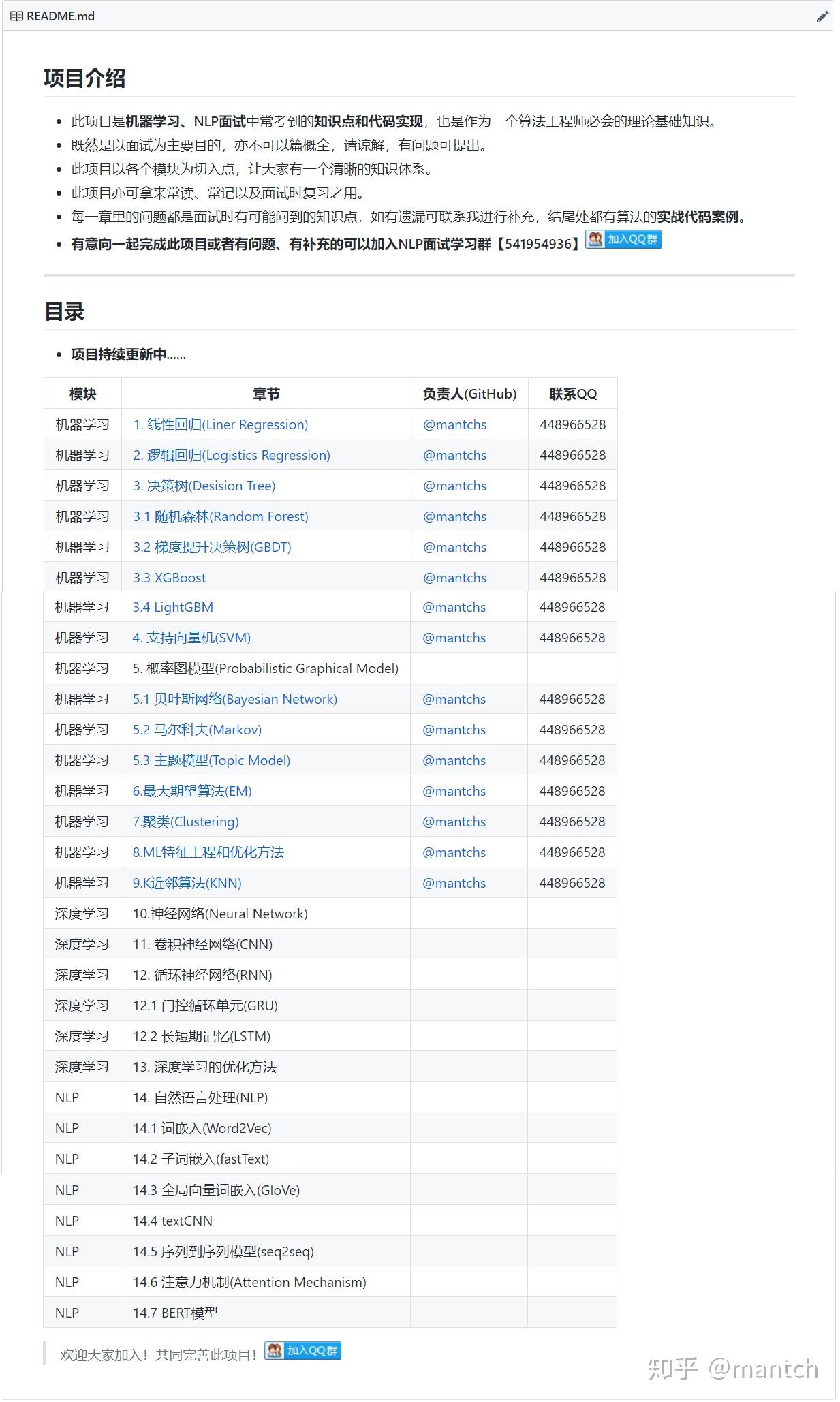
主要思想:投影后类内方差最小,类间方差最大,使得数据在低维度投影之后,同一类别数据的点尽可能接近,不同类别点的类中心尽可能的远。选择投影的方向是能够使数据的类别完全区分开的方向。
输入:数据集  ,其中任意样本
,其中任意样本  为n维向量,
为n维向量,  ,降维到的维度d
,降维到的维度d
输出:降维后的样本集 
1) 计算类内散度矩阵 
2) 计算类间散度矩阵 
3) 计算矩阵 
4) 计算  的最大的d个特征值和对应的d个特征向量
的最大的d个特征值和对应的d个特征向量  ,得到投影矩阵
,得到投影矩阵 
5) 对样本集中的每一个样本特征  ,转化为新的样本
,转化为新的样本 
6) 得到输出样本集 
相同点:
1)二者都可以对数据进行降维
2)降维时都用了矩阵特征分解的思想
3)都假设了数据符合高斯分布
不同点:
1)LDA在降维外还可以用来分类
2)LDA是监督的降维,PCA是无监督的降维
3)LDA最多降到类别数  的维度数,PCA没有限制
的维度数,PCA没有限制
4)LDA选择分类最好的方向进行投影,PCA选择数据具有最大方差的方向进行投影
主要思想:NCA是一种基于stochastic KNN的监督学习,在衡量近邻相似度时借助了度量学习的方法,采用留一法交叉验证,NCA利用目标优化可以对输入数据进行有效的降维。
输入:数据集  ,其中任意样本
,其中任意样本  为n维向量,
为n维向量, 
输出:投影矩阵A,优化目标分数 
1)计算样本近邻分布(降维到低维空间,再计算欧式距离), 
2) 将第i个样本预测为  ,预测第i个正确的概率\(P_i=\sum\limits_{j\in C_i}P_{ij}\)
,预测第i个正确的概率\(P_i=\sum\limits_{j\in C_i}P_{ij}\) 
3) 优化目标 
4)利用梯度更新A,
5)重复上述步骤,直至  最小
最小
NCA在计算距离时,不再仅仅是计算欧式距离,而是借助度量学习中马氏距离的概念,  ,存在
,存在 
 , 最后的优化目标对A求梯度得到
, 最后的优化目标对A求梯度得到 
 , 通过限制A为一个低秩的矩阵
, 通过限制A为一个低秩的矩阵  ,可以对输入数据进行降维,因为优化是非凸优化问题,A是通过不断迭代而得到,变换后的输入被限制在d维。
,可以对输入数据进行降维,因为优化是非凸优化问题,A是通过不断迭代而得到,变换后的输入被限制在d维。
相同点:
1)二者都可以对数据进行降维
2)降维后的维度都需要人工指定
3)二者都可以有效地低维可视化数据
不同点:
1)NCA是监督的降维,PCA是无监督的降维
2)NCA是通过不断迭代优化,学习出投影矩阵A
3)NCA可以减少之后KNN模型学习时的内存和搜索开销
数据集的可视化效果,从上到下依次是“同心环”,“酒”,“人脸”,“数字”数据集,维度从3,13,560,256降至2维展示(图片来源[3])
[1] Wold, Svante, Kim Esbensen, and Paul Geladi. “Principal component analysis.” Chemometrics and intelligent laboratory systems 2.1-3 (1987): 37-52.
[2] Fisher, R. A. (1936). “The Use of Multiple Measurements in Taxonomic Problems” (PDF). Annals of Eugenics. 7 (2): 179–188.
[3] J. Goldberger, G. Hinton, S. Roweis, R. Salakhutdinov. (2005) Neighbourhood Components Analysis. Advances in Neural Information Processing Systems. 17, 513-520, 2005.
这里的sentence2vec指的不是Distributed representations of Sentences and Documents这一篇论文提到的doc2vec的思路,而是更加广义也是在业务中更加经常需要面对的对于每一个样本的item集合进行embedding的方法;还是以典型的app list为例,我们对app进行embedding之后,因为每个用户使用app 长度往往不一致,那么为了下游的gbdt、lr之类的传统机器学习模型能够正常训练我们需要避开数据对其的问题就无法使用concat的方式来合并训练完毕之后的embedding,因此我们需要使用一些策略或者新的算法来处理:
基于传统的统计方法:
1、词袋;
2、tfidf;
3、lsa、plsa、lda、HDP等主题模型
4、LSH
这些都不需要详细介绍了,
本文主要针对于word2vec得到词向量之后如何通过不同的策略来得到sentence的向量,关于这类策略,可以参考github上的一个对标gensim的非常好的高性能sentence embedding实现,下面对照其文档介绍一下:
oborchers/Fast_Sentence_Embeddings1、对句子中所有词的word vector求平均,获得sentence embedding;
思路很简单不赘述了,fse提供了非常方便的实现:
from gensim.models import FastText sentences = [[“cat”, “say”, “meow”], [“dog”, “say”, “woof”]] ft = FastText(sentences, min_count=1, size=10)from fse.models import Average from fse import IndexedList model = Average(ft) model.train(IndexedList(sentences))
只需要将训练完毕的gensim模型放入对应的api中即可,这里推荐使用indexedlist,官方文档提到使用indexdlist是最快的速度载入方式,文本数据的预处理尽量使用其它的方式进行快速处理;
根据源代码的定义,默认是使用cython版的average实现,速度上要比numpy的实现快很多,如果没有安装cython则默认退化为numpy版的average实现。
需要注意的是,在后端,Average会自动判断是word2vec模型还是fasttext的gensim模型,对于word2vec模型来说,正常的average没问题,但是对于fasttext来说,其词向量包括了word的词向量和ngram的词向量,因此,fse在实现上在后端排除了fasttext的ngram embedding,避免计算句子embedding的时候将ngram的embedding也一起计算进去。
作者给出的原因是:
# NOTE: For Fasttext: Use wv.vectors_vocab
# Using the wv.vectors from fasttext had horrible effects on the sts results
# I suspect this is because the wv.vectors are based on the averages of
# wv.vectors_vocab + wv.vectors_ngrams, which will all point into very
# similar directions.
2、基于特定的词频进行加权平均,典型的例如基于tfidf进行加权平均获得sentence embedding
讯享网from gensim.models import FastText sentences = [[“cat”, “say”, “meow”], [“dog”, “say”, “woof”]] ft = FastText(sentences, min_count=1, size=10)
from fse.models import Average from fse import IndexedList model = Average(ft) model.word_weights=XXXXX model.train(IndexedList(sentences))
average默认是用1作为每一个词向量的权重,在这里可以自己进行修改,然后train即可
3、SIF;
具体原理可见:
马东什么:SIF—tfidf+w2v的升级版from gensim.models import FastText sentences = [[“cat”, “say”, “meow”], [“dog”, “say”, “woof”]] ft = FastText(sentences, min_count=1, size=10)from fse.models import SIF from fse import IndexedList model = SIF(ft) model.train(IndexedList(sentences))
讯享网 model : :class:`~gensim.models.keyedvectors.BaseKeyedVectors` or :class:`~gensim.models.base_any2vec.BaseWordEmbeddingsModel` This object essentially contains the mapping between words and embeddings. To compute the sentence embeddings the wv.vocab and wv.vector elements are required. alpha : float, optional Alpha is the weighting factor used to downweigh each individual word. components : int, optional Corresponds to the number of singular vectors to remove from the sentence embeddings. cache_size_gb : float, optional Cache size for computing the singular vectors in GB. sv_mapfile_path : str, optional Optional path to store the sentence-vectors in for very large datasets. Used for memmap. wv_mapfile_path : str, optional Optional path to store the word-vectors in for very large datasets. Used for memmap. Use sv_mapfile_path and wv_mapfile_path to train disk-to-disk without needing much ram. workers : int, optional Number of working threads, used for multithreading. For most tasks (few words in a sentence) a value of 1 should be more than enough. lang_freq : str, optional Some pre-trained embeddings, i.e. "GoogleNews-vectors-negative300.bin", do not contain information about the frequency of a word. As the frequency is required for estimating the word weights, we induce frequencies into the wv.vocab.count based on :class:`~wordfreq` If no frequency information is available, you can choose the language to estimate the frequency. See https://github.com/LuminosoInsight/wordfreq</code></pre></div><p data-pid="_-Uag-Ea">调用和对应参数,底层也是用truncatedsvd来提取第一主成分。</p><p class="ztext-empty-paragraph"><br/></p><p data-pid="JIDwwUub">4、uSIF 改进版sif</p><p class="ztext-empty-paragraph"><br/></p><p class="ztext-empty-paragraph"><br/></p><p data-pid="Gsr6QYFh">待续</p><p></p><p></p><p></p><p></p>
本文约1700字,建议阅读6分钟本文的数据来自美国著名电视节目《老友记》。作者用python-Beautiful Soup抓取了224集中六个主要角色的全部剧本。角色有Ross Geller,Rachel Green,Monica Geller,Phoebe Buffay,Joey Tribbiani和Chandler Bing。本文将使用LDA对《老友记》进行主题建模。
标签:自然语言处理数据可视化,主题建模
流行的主题建模算法包括潜在语义分析*(LSA),层次狄利克雷过程*(HDP)和潜在狄利克雷分配*(LDA),其中LDA在实践中由于效果出众被广泛采用。
主题模型是一组算法/统计模型,可以揭示文档集中的隐藏主题。例如,“浪漫”,“恐怖”和“家庭”将在与电影有关的文档中更频繁地出现。“技术”,“计算机”和“算法”在计算机科学文档中的出现频率会更高。
pyLDAvis
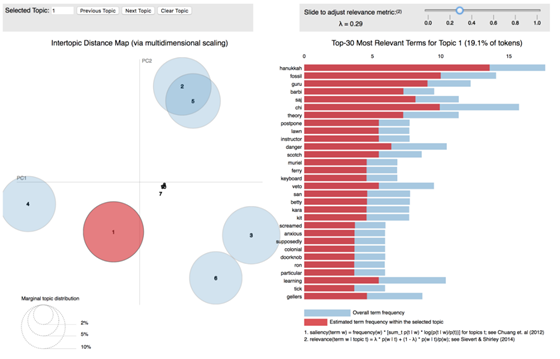
pyLDAvis是一个交互式LDA可视化python软件包。我的LDA建模结果是什么样的?我截取了一个pyLDAvis结果图,如下图所示。圆圈区域表示每个主题在整个语料库中的重要性,圆圈中心之间的距离表示主题之间的相似性。对于每个主题,右侧的直方图列出了前30个最相关的字词。LDA帮助我提取了6个主要主题。以该主题为例,我看到的最相关的术语是光明节(hanukkah),化石(fossil),古鲁(guru)等。对于我们的古生物学家,教授和Geller博士而言,这很可能是一个主题。我已将pyLDAvis分析结果保存为.html文件,您可以从GitHubrepo(https://github.com/XuanX111/Friends_text_generator/blob/master/friend_lda.html)下载它。我是如何得到这个很酷的视觉效果的?接下来我将逐步解释该过程。
自然语言处理
在处理句子之前,我首先将舞台指导与实际对话分开,然后将它们分别存储到pandas Dataframe中。
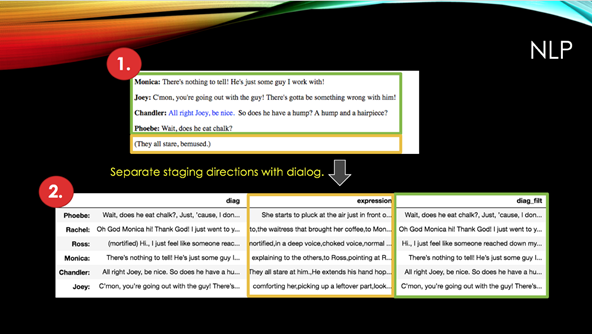
现在,我有六个文档,每个文档包含各个演员说的所有句子。在分词,复词之后,我进一步过滤了停用词(例如a,on,and等),只选择三个以上字母的词。然后,我计算文档中每个单词的出现次数,此过程也称为词袋模型(bag-of-words)。我使用python软件包Gensim(https://radimrehurek.com/gensim/models/ldamodel.html)进行了LDA分析。笔记本和代码可以在我的repo(https://github.com/XuanX111/Friends_text_generator/blob/master/Friends_LDAvis_Xuan_Qi.ipynb)中找到。
有趣的发现
我意识到,即使在《老友记》的角色中,其角色性格的动态特点也可以被探索。Rachel的性格随着剧情的推进而得到发展。在第1季中,Rachel只是一个试图探索世界的被宠坏的富家女孩。但到第6季,她逐渐成长为坚强独立的女性。她所使用的词随着角色的变化而变化,这可以通过LDA主题模型反映出来。我通过按“季”解析.txt文件生成了10 * 6个文档。《老友记》中共有10季和6个主要角色,因此我拥有的文档包括第1季,第2季…的Rachel,第1季,第2季的Chandler等。
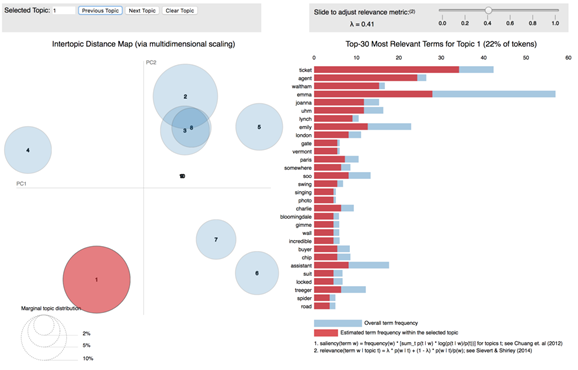
经过50次迭代后,RachelLDA模型帮助我提取了8个主要主题(如上图)。主题之间存在一些重叠,但是通常来讲,LDA主题模型可以帮助我掌握趋势。
思考总结
有多少个主题可供选择?或如何评估LDA模型。
潜在的狄利克雷分配是在未标记的文件上训练的。因此,人们不禁想知道如何评估这种非监督模型?LDA通常要么是通过测量某些次级任务(例如文档分类或信息检索)的性能来评估的,要么是通过给定一些训练文档来估计未知保留文档的概率来评估的。通常,更好的模型将提高文档被保留的可能性。有一篇非常好的论文(http://dirichlet.net/pdf/wallach09evaluation.pdf)介绍了评估LDA模型的各种方法。
评估主题模型是否良好的另一种方法是遵循自己的直觉。当你拥有一个不错的模型时,通常可以讲一个有关所生成的主题的故事。以我的主题模型为例,经过50次迭代,我分配了10个主题。当我进入每个主题时,我有6个主要主题,我发现大多数单词确实与一个字符相关。例如,在主题4中,我看到了Gavin,他曾经是碰巧喜欢Rachel的一位同事。Kim·是Rachel的前任老板。Rachel曾经在Bloomingdale工作。她确实很八卦。如下图所示,主题4中的大多数单词都以字符Rachel为中心。我可以围绕主题讲一个有关的故事,这说明我的模型很好。
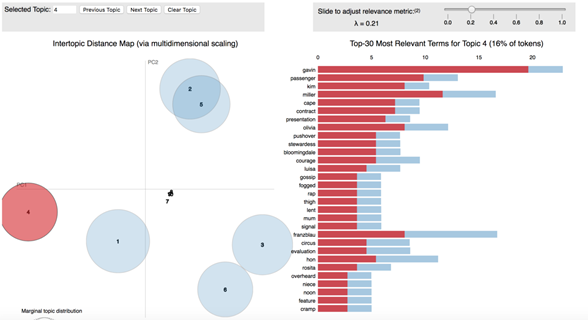
备注:
潜在语言分析(Latent Semantic Analysis,简称:LSA):是自然语言处理中的一种技术,它通过产生与文档和术语相关的一组概念来分析文档和它们包含的术语之间的关系,尤其是分布式语义。
层次狄利克雷过程(hierarchical Dirichlet process,简称HDP):是一种非参数贝叶斯方法,用于对分组数据进行聚类。此方法允许组通过组之间的群集共享来共享统计强度。
潜在狄利克雷分布(the latent Dirichlet allocation,简称LDA):是一种生成统计模型,该模型允许由未观察组解释观察集,这些观察组解释了为什么数据的某些部分相似。
原文标题:
LDA Topic Modeling and pyLDAvis Visualization
原文链接:
https://medium.com/@sherryqixuan/topic-modeling-and-pyldavis-visualization-86a543e21f58
作者:Xuan Qi
翻译:方星轩
- 数据维数
- 数据降维
- 降维方法
- 主成分分析
- 概述
- 算法原理
- 算法步骤
- 应用
- 利用 PCA 处理高维数据
- 概率主成分分析
- 讨论
- PCA的优点
- PCA的局限性
- PCA vs. LDA
- 核主成分分析
- 等距映射(ISO-Metric Mapping)
- 概述
- 计算步骤
- 优缺点
- 局部线性嵌入
- Local Linear Embedding (LLE)
- 计算过程
- 简单例子
机器学习领域中所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中。

维数 (又称维度)
- 数学中:独立参数的数目
- 物理中:独立时空坐标的数目
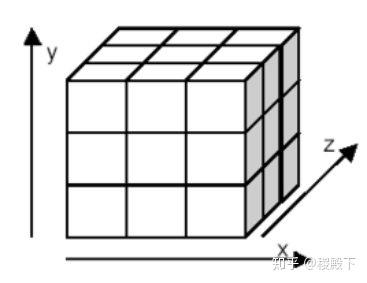
例 “点是0维、直线是1维、平面是2维、体是3维”
- 点基于点是 0 维:在点上定位一个点,不需要参数
- 点基于直线是 1 维:在直线上定位一个点,需要 1 个参数
- 点基于平面是 2 维:在平面上定位一个点,需要 2 个参数
- 点基于体是 3 维:在体上定位一个点,需要 3 个参数

又如, 像素数字放入
像素数字放入  像素白板
像素白板

实际上中,可以通过如下操作增加维数:
- 水平 / 垂直的平移变化
- 旋转变化
- 尺度变化
- 形状变化(不同人写作的习惯)
- 光照变换
- ……
这些变换的因素是潜变量(Latent Variables),潜变量在。
- 为什么要降维?
- 在原始的高维空间中,包含冗余信息和噪声信息,会在实际应用中引入误差,影响准确率;而降维可以提取数据内部的本质结构,减少冗余信息和噪声信息造成的误差,提高应用中的精度。
- 降维的好处
- 直观地好处是维度降低了,便于计算和可视化,其更深层次的意义在于有效信息的提取综合及无用信息的摈弃。
- 一个简单的例子
- 噪声:选择一个方向投影过滤噪声
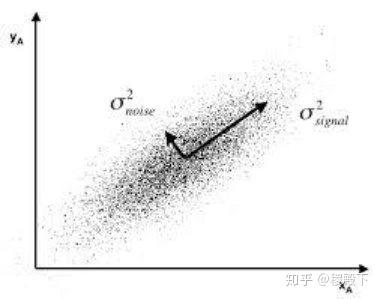
- 冗余
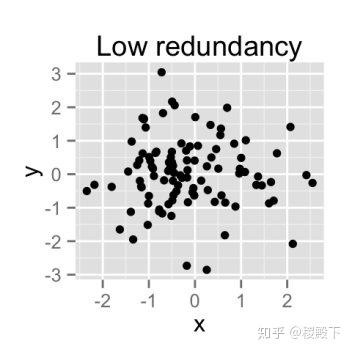
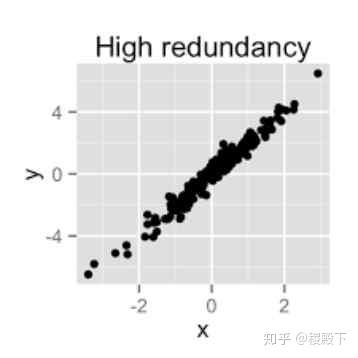
- 降维
- 利用某种映射将原高维度空间的数据点投影到低维度的空间:

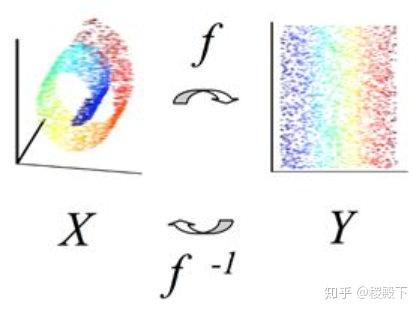
- 降维的本质
- 学习一个映射函数
 ,其中
,其中  是原始数据点的表达,目前最多使用向量表达形式。
是原始数据点的表达,目前最多使用向量表达形式。  是数据点映射后的低维向量表达,通常
是数据点映射后的低维向量表达,通常  的维度小于
的维度小于  的维度(当然提高维度也是可以的)。
的维度(当然提高维度也是可以的)。 可能是显式的或隐式的、线性的或非线性的。
可能是显式的或隐式的、线性的或非线性的。
- 主成分分析(Principal Component Analysis)
- 等距映射(Isometric Mapping)
- 局部线性嵌入(Locally Linear Embedding)
- ……
主成分分析(Principal Component Analysis, PCA),将原有众多具有一定相关性的指标重新组合成一组少量互相无关的综合指标。
- K. Pearson (1901年论文) 针对非随机变量
- H. Hotelling (1933年论文) 推广到随机向量
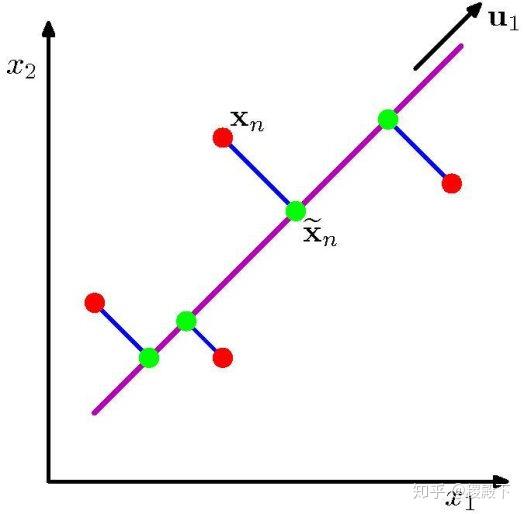
- 使得降维后样本的方差尽可能大
- 使得降维后数据的均方误差尽可能小
例 将维数据集
降为
维,其中

最大方差思想:使用较少的数据维度保留住较多的原数据特性
首先考虑  ,定义这个空间的投影方向为
,定义这个空间的投影方向为  维向量
维向量  ,出于方便且不失一般性,令
,出于方便且不失一般性,令  ,即
,即  为单位向量。则
为单位向量。则
- 每个数据点
 在新空间中表示为标量
在新空间中表示为标量 
- 样本均值在新空间中表示为
 ,其中
,其中

- 投影后样本方差尽可能大,表示为

其中,原样本方差为
 https://www.zhihu.com/equation?tex=%5Cbegin%7Bequation%2A%7D+%5Ccolor%7Bblue%7D+S+%3D+%5Cfrac%7B1%7D%7BN%7D+%5Csum_%7Bn%3D1%7D%5E%7BN%7D%5Cleft%28x_n+-+%5Cbar%7Bx%7D+%5Cright%29%5E2+%5Cend%7Bequation%2A%7D+%5C%5C” alt=“\begin{equation} \color{blue} S = \frac{1}{N} \sum_{n=1}^{N}\left(x_n - \bar{x} \right)^2 \end{equation} \” eeimg=“1”/>
https://www.zhihu.com/equation?tex=%5Cbegin%7Bequation%2A%7D+%5Ccolor%7Bblue%7D+S+%3D+%5Cfrac%7B1%7D%7BN%7D+%5Csum_%7Bn%3D1%7D%5E%7BN%7D%5Cleft%28x_n+-+%5Cbar%7Bx%7D+%5Cright%29%5E2+%5Cend%7Bequation%2A%7D+%5C%5C” alt=“\begin{equation} \color{blue} S = \frac{1}{N} \sum_{n=1}^{N}\left(x_n - \bar{x} \right)^2 \end{equation} \” eeimg=“1”/>
该约束优化问题可表述为
 https://www.zhihu.com/equation?tex=%5Cbegin%7Bequation%2A%7D+%5Cbegin%7Baligned%7D+%5Cmax_%7Bu_1%5Cin%5Cmathbb%7BR%7D%5EM%7D+~~%26+u_1%5ETSu_1+%5C%5C+%5Cmathrm%7Bs.t.%7D+~~%26+u_1%5ETu_1+%3D+1+%5Cend%7Baligned%7D+%5Cend%7Bequation%2A%7D+%5C%5C” alt=“\begin{equation} \begin{aligned} \max_{u_1\in\mathbb{R}^M} ~~& u_1^TSu_1 \ \mathrm{s.t.}
https://www.zhihu.com/equation?tex=%5Cbegin%7Bequation%2A%7D+%5Cbegin%7Baligned%7D+%5Cmax_%7Bu_1%5Cin%5Cmathbb%7BR%7D%5EM%7D+~~%26+u_1%5ETSu_1+%5C%5C+%5Cmathrm%7Bs.t.%7D+~~%26+u_1%5ETu_1+%3D+1+%5Cend%7Baligned%7D+%5Cend%7Bequation%2A%7D+%5C%5C” alt=“\begin{equation} \begin{aligned} \max_{u_1\in\mathbb{R}^M} ~~& u_1^TSu_1 \ \mathrm{s.t.} & u_1^Tu_1 = 1 \end{aligned} \end{equation*} \” eeimg=“1”/>
利用拉格朗日乘子法,构造 Lagrange 函数

对  求偏导并令偏导数为 0,有
求偏导并令偏导数为 0,有

即

结论: 是
是  的特征向量。进一步,有
的特征向量。进一步,有

即  是
是  最大特征值对应的特征向量时,方差取到最大值,称
最大特征值对应的特征向量时,方差取到最大值,称  为第一主成分。
为第一主成分。
- 最小均方误差思想:使原数据与降维后的数据 (在原空间中的重建) 的误差最小
考虑更一般性的情况( ), 新空间中数据方差最大的**投影方向由协方差矩阵
), 新空间中数据方差最大的**投影方向由协方差矩阵  的
的  个特征向量定义, 其分别对应
个特征向量定义, 其分别对应  个最大的特征值
个最大的特征值  。
。
- 首先获得方差最大的1维,生成该维的补空间;
- 继续在补空间中获得方差最大的1维,生成新的补空间;
- 依次循环下去得到M维的空间
定义一组单位正交的  维基向量
维基向量  ,满足
,满足

由于基是完全的,每个数据点可以表示为基向量的线性组合

相当于进行了坐标转换
 https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+%5C%7Bx_%7Bn1%7D%2Cx_%7Bn2%7D%2C%5Ccdots%2Cx_%7BnD%7D%5C%7D+%26%5Cmathop%7B%5Clongrightarrow%7D%5E%7B%5C%7Bu_i%5C%7D%7D+%5C%7B%5Calpha_%7Bn1%7D%2C%5Calpha_%7Bn2%7D%2C%5Ccdots%2C%5Calpha_%7BnD%7D%5C%7D+%5C%5C+%26%5CDownarrow+%5C%5C+%5Calpha_%7Bnj%7D+%26%3D+x_n%5ETuj+%5Cend%7Baligned%7D+%5C%5C” alt=“\begin{aligned} {x{n1},x{n2},\cdots,x{nD}} &\mathop{\longrightarrow}^{{ui}} {\alpha{n1},\alpha{n2},\cdots,\alpha{nD}} \ &
https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+%5C%7Bx_%7Bn1%7D%2Cx_%7Bn2%7D%2C%5Ccdots%2Cx_%7BnD%7D%5C%7D+%26%5Cmathop%7B%5Clongrightarrow%7D%5E%7B%5C%7Bu_i%5C%7D%7D+%5C%7B%5Calpha_%7Bn1%7D%2C%5Calpha_%7Bn2%7D%2C%5Ccdots%2C%5Calpha_%7BnD%7D%5C%7D+%5C%5C+%26%5CDownarrow+%5C%5C+%5Calpha_%7Bnj%7D+%26%3D+x_n%5ETuj+%5Cend%7Baligned%7D+%5C%5C” alt=“\begin{aligned} {x{n1},x{n2},\cdots,x{nD}} &\mathop{\longrightarrow}^{{ui}} {\alpha{n1},\alpha{n2},\cdots,\alpha{nD}} \ &\Downarrow \ \alpha_{nj} &= x_n^Tu_j \end{aligned} \” eeimg=“1”/>
则


在  维变量(\(M <img src="https://www.zhihu.com/equation?tex=%5Ctilde%7Bx%7D_n+%3D+%5Csum_%7Bi%3D1%7D%5EM+%7B%5Ccolor%7Bred%7Dz_%7Bni%7D%7Du_i+%2B+%5Csum_%7Bi+%3D+M%2B1%7D%5ED+%7B%5Ccolor%7Bmagenta%7Db_i%7D+u_i+%5C%5C" alt="\tilde{x}_n = \sum_{i=1}^M {\color{red}z_{ni}}u_i + \sum_{i = M+1}^D {\color{magenta}b_i} u_i \\" eeimg="1"/> </p><p data-pid="ydLYjZ5Z">目标为最小化失真率</p><p data-pid="c-doiXl1"><img src="https://www.zhihu.com/equation?tex=%5Cmin+~J+%3D+%5Cmin~%5Cfrac%7B1%7D%7BN%7D+%5Csum_%7Bn%3D1%7D%5EN%5C%7C+x_n+-+%5Ctilde%7Bx%7D_n+%5C%7C%5E2+%5C%5C" alt="\min ~J = \min~\frac{1}{N} \sum_{n=1}^N\| x_n - \tilde{x}_n \|^2 \\" eeimg="1"/></p><p data-pid="MVdKGI-s">导数置为 0 得</p><p data-pid="g_V5C6s4"><img src="https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+z_%7Bnj%7D+%26%3D+x_n%5ET+u_j%2C+j+%3D+1%2C2%2C%5Ccdots%2CM+%5C%5C+b_j+%26%3D+%5Cbar%7Bx%7D%5ET+u_j%2Cj%3DM%2B1%2C%5Ccdot%2C%5Ccdots%2CD+%5Cend%7Baligned%7D+%5C%5C" alt="\begin{aligned} z_{nj} &= x_n^T u_j, j = 1,2,\cdots,M \\ b_j &= \bar{x}^T u_j,j=M+1,\cdot,\cdots,D \end{aligned} \\" eeimg="1"/></p><p data-pid="NPYVXYxh">则有</p><p data-pid="tPh6IV02"><img src="https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+x_n+-+%5Ctilde%7Bx%7D_n+%26%3D+%5Csum_%7Bi%3DM%2B1%7D%5ED%5C%7B+%28x_n-%5Cbar%7Bx%7D%29%5ET+u_i+%5C%7D+u_i+%5Cend%7Baligned%7D+%5C%5C" alt="\begin{aligned} x_n - \tilde{x}_n &= \sum_{i=M+1}^D\{ (x_n-\bar{x})^T u_i \} u_i \end{aligned} \\" eeimg="1"/></p><p data-pid="_BNE68GE">即</p><p data-pid="957jBgD9"><img src="https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D++J+%26%3D+%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bn%3D1%7D%5EN+%5Csum_%7BM%2B1%7D%5ED+%5Cleft%28x_n%5ETu_i+-+%5Cbar%7Bx%7D%5ETu_i%5Cright%29%5E2+%5C%5C+%26%3D%5Csum_%7Bi%3DM%2B1%7D%5EDu_i%5ETSu_i++%5Cend%7Baligned%7D+%5C%5C" alt="\begin{aligned} J &= \frac{1}{N}\sum_{n=1}^N \sum_{M+1}^D \left(x_n^Tu_i - \bar{x}^Tu_i\right)^2 \\ &=\sum_{i=M+1}^Du_i^TSu_i \end{aligned} \\" eeimg="1"/></p><p data-pid="J_e73OvF">构造拉格朗日函数,得</p><p data-pid="pwKuNTaL"><img src="https://www.zhihu.com/equation?tex=%5Cmathcal%7BL%7D+%3D%5Csum_%7Bi%3DM%2B1%7D%5EDu_i%5ETSu_i+%2B+%5Csum_%7Bi%3DM%2B1%7D%5ED%5Clambda_i+%281-u_i%5ETu_i%29+%5C%5C" alt="\mathcal{L} =\sum_{i=M+1}^Du_i^TSu_i + \sum_{i=M+1}^D\lambda_i (1-u_i^Tu_i) \\" eeimg="1"/></p><p data-pid="cDad1Soc">对 <img src="https://www.zhihu.com/equation?tex=u_i" alt="u_i" eeimg="1"/> 求偏导,并置为 0 得</p><p data-pid="-9F_2WvV"><img src="https://www.zhihu.com/equation?tex=S+u_i+%3D+%5Clambda_i+u_i+%5C%5C" alt="S u_i = \lambda_i u_i \\" eeimg="1"/></p><p data-pid="vYve7BIx"><img src="https://www.zhihu.com/equation?tex=J" alt="J" eeimg="1"/> 最小时取 <img src="https://www.zhihu.com/equation?tex=D-M" alt="D-M" eeimg="1"/> 个最小得特征值。对应的失真度为</p><p data-pid="SZxX6rJR"><img src="https://www.zhihu.com/equation?tex=J+%3D+%5Csum_%7Bi+%3D+M%2B1%7D%5ED+%5Clambda_i+%5C%5C" alt="J = \sum_{i = M+1}^D \lambda_i \\" eeimg="1"/></p><ul><li data-pid="WwtDsZMj">计算给定样本 <img src="https://www.zhihu.com/equation?tex=%5C%7Bx_n%5C%7D%2Cn%3D1%2C2%2C%5Ccdots%2CN" alt="\{x_n\},n=1,2,\cdots,N" eeimg="1"/> 的均值 <img src="https://www.zhihu.com/equation?tex=%5Cbar%7Bx%7D" alt="\bar{x}" eeimg="1"/> 和协方差矩阵 <img src="https://www.zhihu.com/equation?tex=S" alt="S" eeimg="1"/></li><li data-pid="-2snB78v">计算 <img src="https://www.zhihu.com/equation?tex=S" alt="S" eeimg="1"/> 的特征向量与特征值</li><li data-pid="lid5W0iG">将特征值从大到小排列,前 <img src="https://www.zhihu.com/equation?tex=M" alt="M" eeimg="1"/> 个特征值 <img src="https://www.zhihu.com/equation?tex=%5Clambda_1%2C%5Clambda_2%2C%5Ccdots%2C%5Clambda_M" alt="\lambda_1,\lambda_2,\cdots,\lambda_M" eeimg="1"/> 所对应的特征向量 <img src="https://www.zhihu.com/equation?tex=u_1%2Cu_2%2C%5Ccdots%2Cu_M" alt="u_1,u_2,\cdots,u_M" eeimg="1"/> 构成投影矩阵</li></ul><figure data-size="normal"><img src="https://pic2.zhimg.com/v2-5a3aa53ca0cd5d40cf4be3821_b.jpg" data-caption="" data-size="normal" data-rawwidth="377" data-rawheight="357" class="content_image" width="377"/></figure><figure data-size="normal"><img src="https://pic3.zhimg.com/v2-f76ea11d21a95b97c916cb0afe_r.jpg" data-caption="" data-size="normal" data-rawwidth="748" data-rawheight="419" class="origin_image zh-lightbox-thumb" width="748" data-original="https://pic3.zhimg.com/v2-f76ea11d21a95b97c916cb0afe_r.jpg"/></figure><figure data-size="normal"><img src="https://picx.zhimg.com/v2-d657dff617aa336b6d4f2211f711b71f_r.jpg" data-caption="" data-size="normal" data-rawwidth="1424" data-rawheight="324" class="origin_image zh-lightbox-thumb" width="1424" data-original="https://picx.zhimg.com/v2-d657dff617aa336b6d4f2211f711b71f_r.jpg"/></figure><p data-pid="0yNOW_T-">特征值分布谱特征值由大到小排列,如下</p><figure data-size="normal"><img src="https://pic4.zhimg.com/v2-37b438d01cca07fe1d6c9a96d10dd619_r.jpg" data-caption="" data-size="normal" data-rawwidth="721" data-rawheight="538" class="origin_image zh-lightbox-thumb" width="721" data-original="https://pic4.zhimg.com/v2-37b438d01cca07fe1d6c9a96d10dd619_r.jpg"/></figure><p data-pid="Yzeq8ng5">选取前 <img src="https://www.zhihu.com/equation?tex=M" alt="M" eeimg="1"/> 个特征值进行降维,有如下结果</p><figure data-size="normal"><img src="https://pic3.zhimg.com/v2-22bfe49c38c0f8836e04c79c7b042e24_r.jpg" data-caption="" data-size="normal" data-rawwidth="1424" data-rawheight="325" class="origin_image zh-lightbox-thumb" width="1424" data-original="https://pic3.zhimg.com/v2-22bfe49c38c0f8836e04c79c7b042e24_r.jpg"/></figure><p data-pid="TMAdT0e9">失真度分布谱随 <img src="https://www.zhihu.com/equation?tex=M" alt="M" eeimg="1"/> 取值由小到大排列,如下:</p><figure data-size="normal"><img src="https://pic2.zhimg.com/v2-ae4ae0a2d52f81ec1f76abe1d7acd033_r.jpg" data-caption="" data-size="normal" data-rawwidth="721" data-rawheight="538" class="origin_image zh-lightbox-thumb" width="721" data-original="https://pic2.zhimg.com/v2-ae4ae0a2d52f81ec1f76abe1d7acd033_r.jpg"/></figure><p data-pid="3ln_vieH">在实际应用中,样本维数可能很高,远大于样本的个数在人脸识别中,1000 张人脸图像,每张图像 <img src="https://www.zhihu.com/equation?tex=100%5Ctimes100" alt="100\times100" eeimg="1"/> 像素。<img src="https://www.zhihu.com/equation?tex=D" alt="D" eeimg="1"/> 维空间,<img src="https://www.zhihu.com/equation?tex=N" alt="N" eeimg="1"/> 个样本点,\)N
维变量(\(M <img src="https://www.zhihu.com/equation?tex=%5Ctilde%7Bx%7D_n+%3D+%5Csum_%7Bi%3D1%7D%5EM+%7B%5Ccolor%7Bred%7Dz_%7Bni%7D%7Du_i+%2B+%5Csum_%7Bi+%3D+M%2B1%7D%5ED+%7B%5Ccolor%7Bmagenta%7Db_i%7D+u_i+%5C%5C" alt="\tilde{x}_n = \sum_{i=1}^M {\color{red}z_{ni}}u_i + \sum_{i = M+1}^D {\color{magenta}b_i} u_i \\" eeimg="1"/> </p><p data-pid="ydLYjZ5Z">目标为最小化失真率</p><p data-pid="c-doiXl1"><img src="https://www.zhihu.com/equation?tex=%5Cmin+~J+%3D+%5Cmin~%5Cfrac%7B1%7D%7BN%7D+%5Csum_%7Bn%3D1%7D%5EN%5C%7C+x_n+-+%5Ctilde%7Bx%7D_n+%5C%7C%5E2+%5C%5C" alt="\min ~J = \min~\frac{1}{N} \sum_{n=1}^N\| x_n - \tilde{x}_n \|^2 \\" eeimg="1"/></p><p data-pid="MVdKGI-s">导数置为 0 得</p><p data-pid="g_V5C6s4"><img src="https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+z_%7Bnj%7D+%26%3D+x_n%5ET+u_j%2C+j+%3D+1%2C2%2C%5Ccdots%2CM+%5C%5C+b_j+%26%3D+%5Cbar%7Bx%7D%5ET+u_j%2Cj%3DM%2B1%2C%5Ccdot%2C%5Ccdots%2CD+%5Cend%7Baligned%7D+%5C%5C" alt="\begin{aligned} z_{nj} &= x_n^T u_j, j = 1,2,\cdots,M \\ b_j &= \bar{x}^T u_j,j=M+1,\cdot,\cdots,D \end{aligned} \\" eeimg="1"/></p><p data-pid="NPYVXYxh">则有</p><p data-pid="tPh6IV02"><img src="https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+x_n+-+%5Ctilde%7Bx%7D_n+%26%3D+%5Csum_%7Bi%3DM%2B1%7D%5ED%5C%7B+%28x_n-%5Cbar%7Bx%7D%29%5ET+u_i+%5C%7D+u_i+%5Cend%7Baligned%7D+%5C%5C" alt="\begin{aligned} x_n - \tilde{x}_n &= \sum_{i=M+1}^D\{ (x_n-\bar{x})^T u_i \} u_i \end{aligned} \\" eeimg="1"/></p><p data-pid="_BNE68GE">即</p><p data-pid="957jBgD9"><img src="https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D++J+%26%3D+%5Cfrac%7B1%7D%7BN%7D%5Csum_%7Bn%3D1%7D%5EN+%5Csum_%7BM%2B1%7D%5ED+%5Cleft%28x_n%5ETu_i+-+%5Cbar%7Bx%7D%5ETu_i%5Cright%29%5E2+%5C%5C+%26%3D%5Csum_%7Bi%3DM%2B1%7D%5EDu_i%5ETSu_i++%5Cend%7Baligned%7D+%5C%5C" alt="\begin{aligned} J &= \frac{1}{N}\sum_{n=1}^N \sum_{M+1}^D \left(x_n^Tu_i - \bar{x}^Tu_i\right)^2 \\ &=\sum_{i=M+1}^Du_i^TSu_i \end{aligned} \\" eeimg="1"/></p><p data-pid="J_e73OvF">构造拉格朗日函数,得</p><p data-pid="pwKuNTaL"><img src="https://www.zhihu.com/equation?tex=%5Cmathcal%7BL%7D+%3D%5Csum_%7Bi%3DM%2B1%7D%5EDu_i%5ETSu_i+%2B+%5Csum_%7Bi%3DM%2B1%7D%5ED%5Clambda_i+%281-u_i%5ETu_i%29+%5C%5C" alt="\mathcal{L} =\sum_{i=M+1}^Du_i^TSu_i + \sum_{i=M+1}^D\lambda_i (1-u_i^Tu_i) \\" eeimg="1"/></p><p data-pid="cDad1Soc">对 <img src="https://www.zhihu.com/equation?tex=u_i" alt="u_i" eeimg="1"/> 求偏导,并置为 0 得</p><p data-pid="-9F_2WvV"><img src="https://www.zhihu.com/equation?tex=S+u_i+%3D+%5Clambda_i+u_i+%5C%5C" alt="S u_i = \lambda_i u_i \\" eeimg="1"/></p><p data-pid="vYve7BIx"><img src="https://www.zhihu.com/equation?tex=J" alt="J" eeimg="1"/> 最小时取 <img src="https://www.zhihu.com/equation?tex=D-M" alt="D-M" eeimg="1"/> 个最小得特征值。对应的失真度为</p><p data-pid="SZxX6rJR"><img src="https://www.zhihu.com/equation?tex=J+%3D+%5Csum_%7Bi+%3D+M%2B1%7D%5ED+%5Clambda_i+%5C%5C" alt="J = \sum_{i = M+1}^D \lambda_i \\" eeimg="1"/></p><ul><li data-pid="WwtDsZMj">计算给定样本 <img src="https://www.zhihu.com/equation?tex=%5C%7Bx_n%5C%7D%2Cn%3D1%2C2%2C%5Ccdots%2CN" alt="\{x_n\},n=1,2,\cdots,N" eeimg="1"/> 的均值 <img src="https://www.zhihu.com/equation?tex=%5Cbar%7Bx%7D" alt="\bar{x}" eeimg="1"/> 和协方差矩阵 <img src="https://www.zhihu.com/equation?tex=S" alt="S" eeimg="1"/></li><li data-pid="-2snB78v">计算 <img src="https://www.zhihu.com/equation?tex=S" alt="S" eeimg="1"/> 的特征向量与特征值</li><li data-pid="lid5W0iG">将特征值从大到小排列,前 <img src="https://www.zhihu.com/equation?tex=M" alt="M" eeimg="1"/> 个特征值 <img src="https://www.zhihu.com/equation?tex=%5Clambda_1%2C%5Clambda_2%2C%5Ccdots%2C%5Clambda_M" alt="\lambda_1,\lambda_2,\cdots,\lambda_M" eeimg="1"/> 所对应的特征向量 <img src="https://www.zhihu.com/equation?tex=u_1%2Cu_2%2C%5Ccdots%2Cu_M" alt="u_1,u_2,\cdots,u_M" eeimg="1"/> 构成投影矩阵</li></ul><figure data-size="normal"><img src="https://pic2.zhimg.com/v2-5a3aa53ca0cd5d40cf4be3821_b.jpg" data-caption="" data-size="normal" data-rawwidth="377" data-rawheight="357" class="content_image" width="377"/></figure><figure data-size="normal"><img src="https://pic3.zhimg.com/v2-f76ea11d21a95b97c916cb0afe_r.jpg" data-caption="" data-size="normal" data-rawwidth="748" data-rawheight="419" class="origin_image zh-lightbox-thumb" width="748" data-original="https://pic3.zhimg.com/v2-f76ea11d21a95b97c916cb0afe_r.jpg"/></figure><figure data-size="normal"><img src="https://picx.zhimg.com/v2-d657dff617aa336b6d4f2211f711b71f_r.jpg" data-caption="" data-size="normal" data-rawwidth="1424" data-rawheight="324" class="origin_image zh-lightbox-thumb" width="1424" data-original="https://picx.zhimg.com/v2-d657dff617aa336b6d4f2211f711b71f_r.jpg"/></figure><p data-pid="0yNOW_T-">特征值分布谱特征值由大到小排列,如下</p><figure data-size="normal"><img src="https://pic4.zhimg.com/v2-37b438d01cca07fe1d6c9a96d10dd619_r.jpg" data-caption="" data-size="normal" data-rawwidth="721" data-rawheight="538" class="origin_image zh-lightbox-thumb" width="721" data-original="https://pic4.zhimg.com/v2-37b438d01cca07fe1d6c9a96d10dd619_r.jpg"/></figure><p data-pid="Yzeq8ng5">选取前 <img src="https://www.zhihu.com/equation?tex=M" alt="M" eeimg="1"/> 个特征值进行降维,有如下结果</p><figure data-size="normal"><img src="https://pic3.zhimg.com/v2-22bfe49c38c0f8836e04c79c7b042e24_r.jpg" data-caption="" data-size="normal" data-rawwidth="1424" data-rawheight="325" class="origin_image zh-lightbox-thumb" width="1424" data-original="https://pic3.zhimg.com/v2-22bfe49c38c0f8836e04c79c7b042e24_r.jpg"/></figure><p data-pid="TMAdT0e9">失真度分布谱随 <img src="https://www.zhihu.com/equation?tex=M" alt="M" eeimg="1"/> 取值由小到大排列,如下:</p><figure data-size="normal"><img src="https://pic2.zhimg.com/v2-ae4ae0a2d52f81ec1f76abe1d7acd033_r.jpg" data-caption="" data-size="normal" data-rawwidth="721" data-rawheight="538" class="origin_image zh-lightbox-thumb" width="721" data-original="https://pic2.zhimg.com/v2-ae4ae0a2d52f81ec1f76abe1d7acd033_r.jpg"/></figure><p data-pid="3ln_vieH">在实际应用中,样本维数可能很高,远大于样本的个数在人脸识别中,1000 张人脸图像,每张图像 <img src="https://www.zhihu.com/equation?tex=100%5Ctimes100" alt="100\times100" eeimg="1"/> 像素。<img src="https://www.zhihu.com/equation?tex=D" alt="D" eeimg="1"/> 维空间,<img src="https://www.zhihu.com/equation?tex=N" alt="N" eeimg="1"/> 个样本点,\)N 
其中  ,显然
,显然  的维度相当大,引起维度灾难。
的维度相当大,引起维度灾难。
又

令  ,得到
,得到

其中  ,显然
,显然  的维度相比
的维度相比  要小的多了。
要小的多了。
因此,需对  进行特征值分解得
进行特征值分解得  和
和  ,所以
,所以

因为  为单位向量,所以
为单位向量,所以

这就是所谓的奇异值分解 (Singular Value Decomposition, SVD)。
- PCA 的概率表示
隐变量  以如下形式产生
以如下形式产生  维观测变量
维观测变量 

其中, 为均值,
为均值, 为高斯噪声。
为高斯噪声。  为
为  维的隐变量,且满足高斯分布
维的隐变量,且满足高斯分布

 以
以  为条件的分布也满足高斯分布
为条件的分布也满足高斯分布

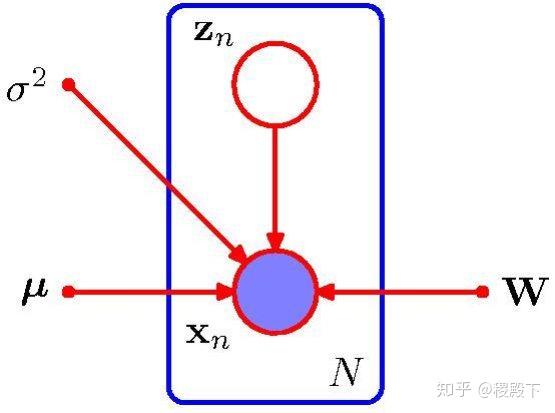
- 从隐空间到数据空间的映射,与 PCA 的传统视角相反
- 从数据空间到隐空间的映射,可以由贝叶斯定理得到
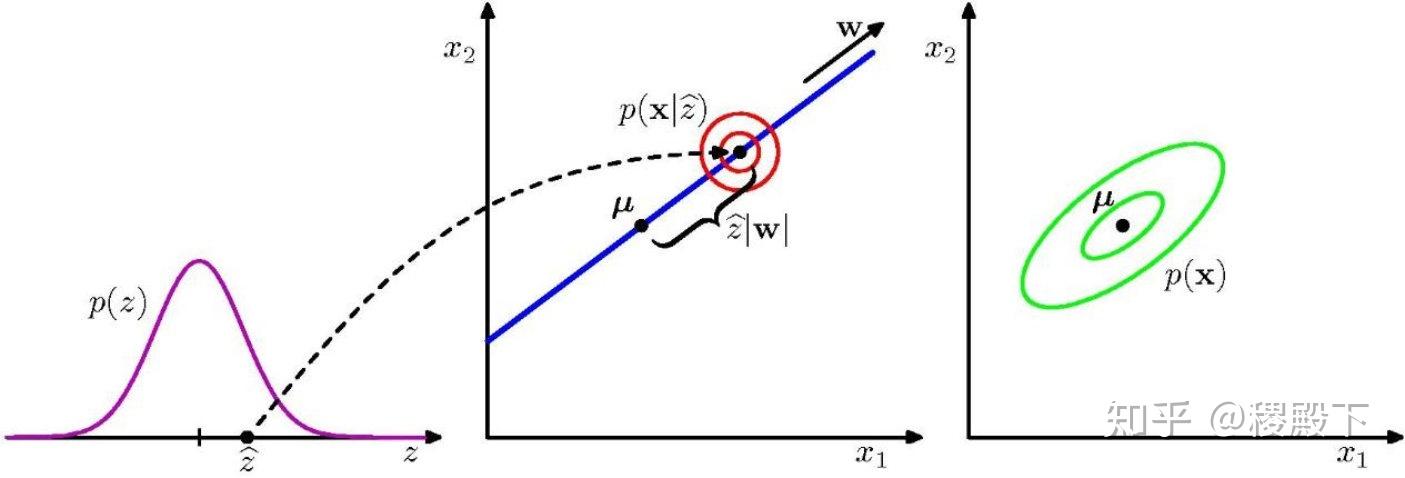
根据贝叶斯定理,有

其中

因此
![\begin{aligned} \mathbb{E}[x] &= \mathbb{E}[Wz + \mu +\epsilon] = \mu \\ \mathrm{cov}[x] &= \mathbb{E}[(Wz+\epsilon)(Wz+\epsilon)^T] \\ &=\mathbb{E}[Wzz^TW^T] + \mathbb{E}[\epsilon\epsilon^T] \\ &=WW^T + \sigma^2I \end{aligned} \\](https://51itzy.com/uploads/202412/23/d8d6e00325d3a7fb.jpg)
一般利用最大似然估计进行求解,给定  ,求其对数似然函数
,求其对数似然函数

对  求导并置为 0 得
求导并置为 0 得

于是,有

代入似然函数,有

其中  为相关矩阵。因此
为相关矩阵。因此

- 具有很高普适性,最大程度地保持了原有数据的信息;
- 可对主元的重要性进行排序,并根据需要略去部分维数,达到降维从而简化模型或对数据进行压缩的效果;
- 完全无参数限制,在计算过程中不需要人为设定参数或是根 据任何经验模型对计算进行干预,最终结果只与数据相关。

- 假设模型是线性的,也就决定了它能进行的主元分析之间的关系也是线性的;
- 假设概率分布模型是指数型;
- 假设数据具有较高信噪比,具有最高方差的一维向量被看作是主元,而方差较小的变化被认为是噪声
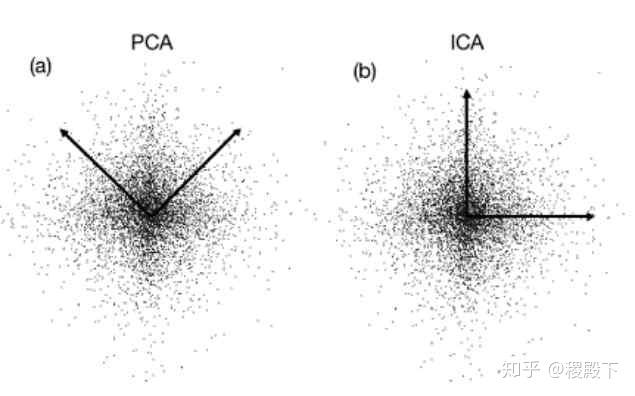
- PCA 追求降维后能够最大化保持数据内在信息,并通过衡量在投影方向上的数据方差来判断其重要性。但这对数据的区分作用并不大,反而可能使得数据点混杂在一起。

- LDA 所追求的目标与 PCA 不同,不是希望保持数据最多的信息,而是希望数据在降维后能够很容易地被区分开。
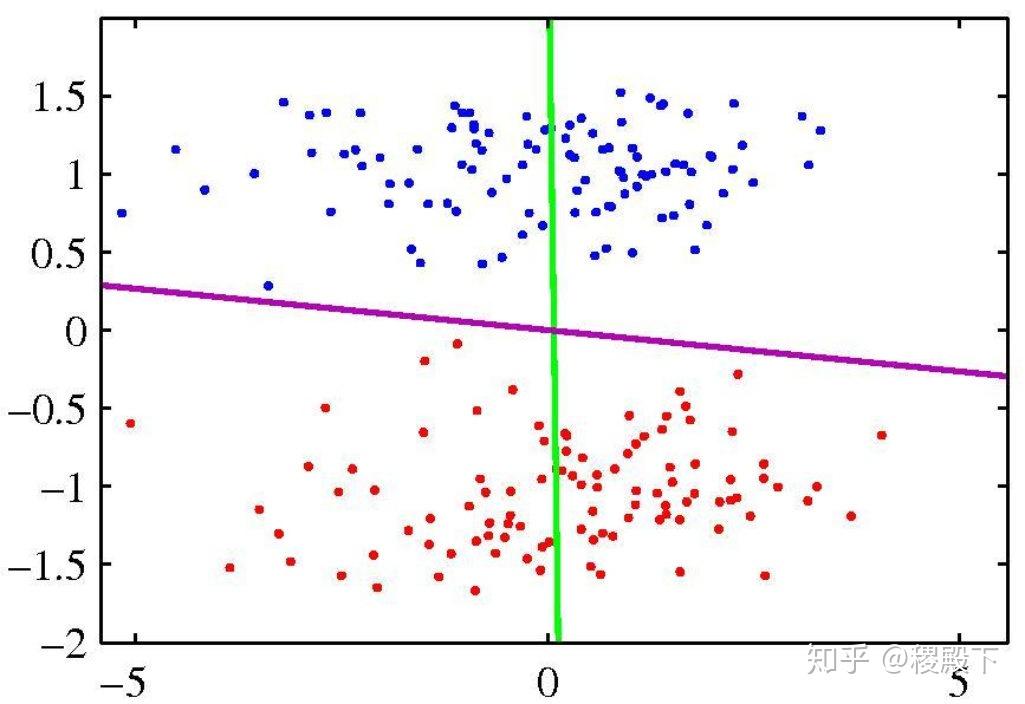
将主成分分析的线性假设一般化使之适应非线性数据
- 传统 PCA:
 维样本
维样本  ,
,

- 核 PCA:非线性映射
 ,
,

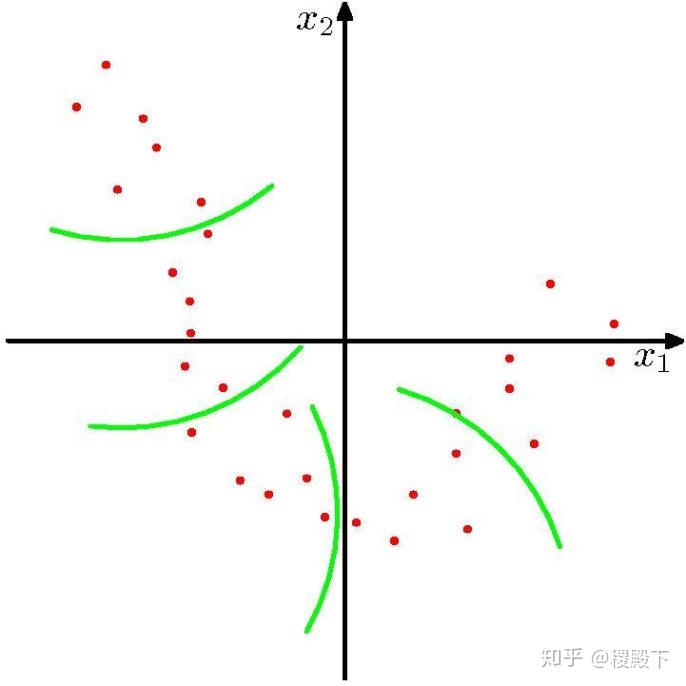
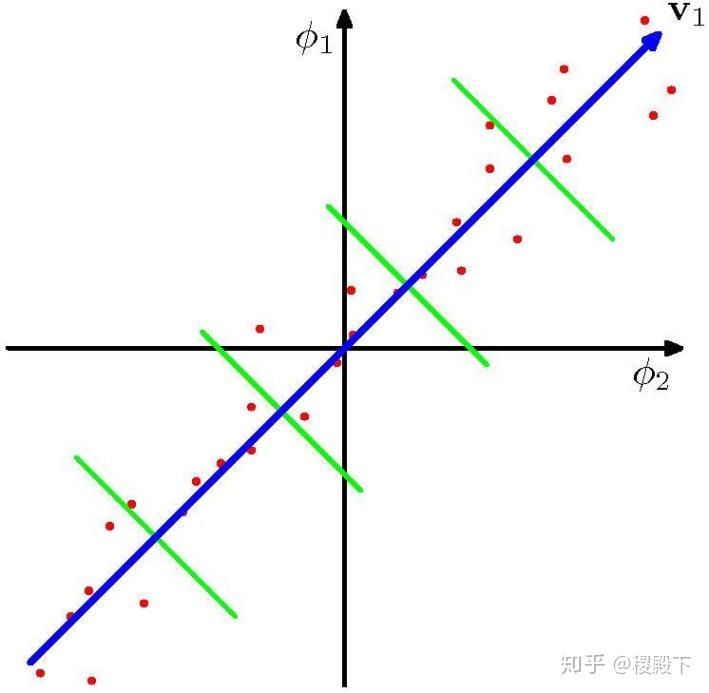
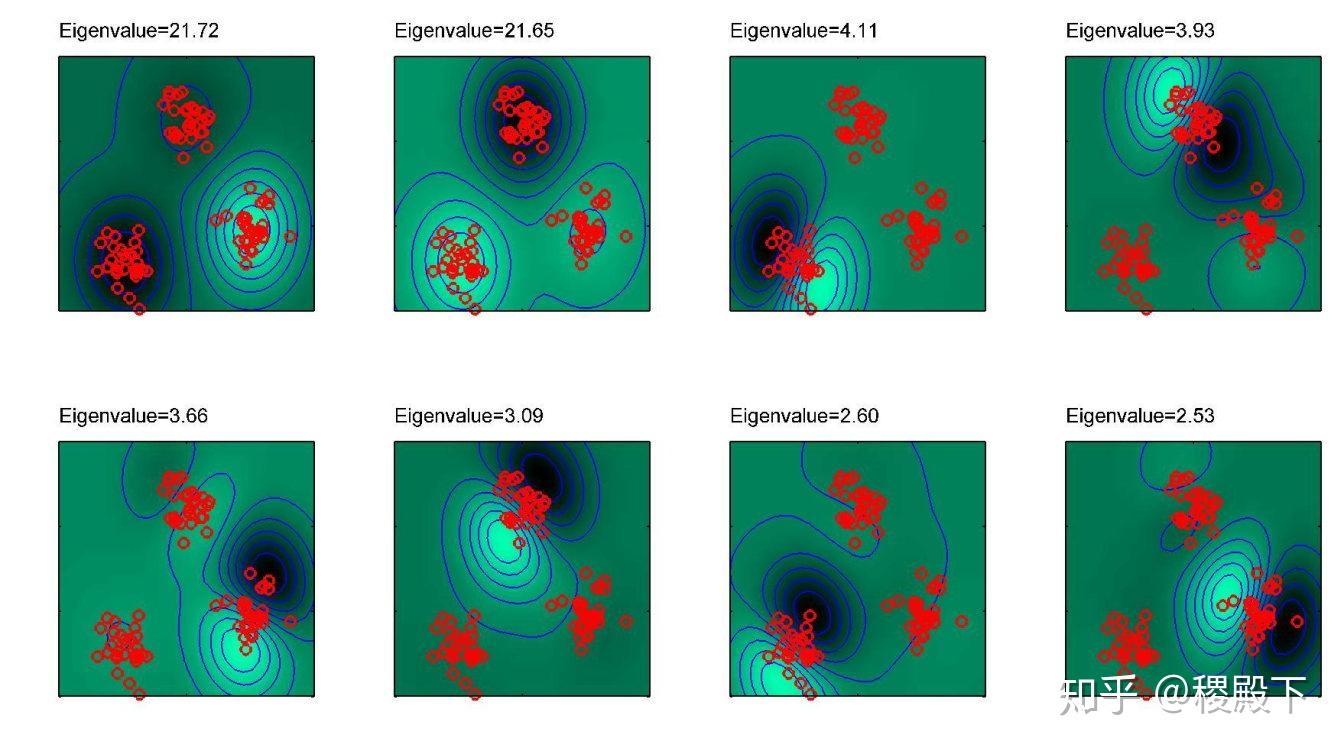
等距映射的思想:保持数据点内在几何性质 (测地距离)
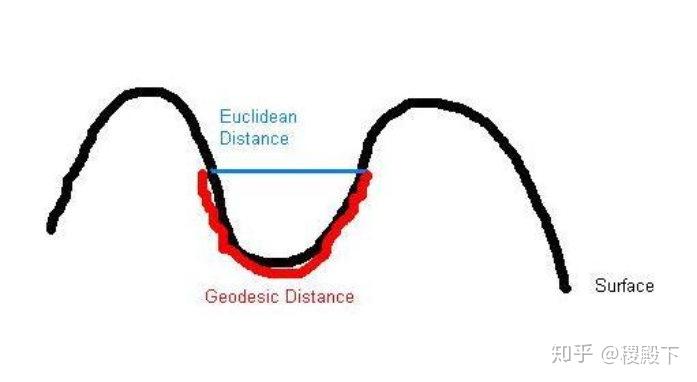
对给定数据  ,构造图
,构造图  。其中
。其中  是顶点集合,
是顶点集合, 是边的集合。若
是边的集合。若  小于某个值
小于某个值  (
( -ISOMAP),或
-ISOMAP),或  是
是  的
的  近邻(
近邻( -ISOMAP),则顶点
-ISOMAP),则顶点  和
和  的边权值设为
的边权值设为  ,否则为 0。
,否则为 0。
计算图  中任意两点间的最短距离,得到矩阵
中任意两点间的最短距离,得到矩阵  ,可选算法有
,可选算法有
- Dijkstra 最短路径算法
- Floyd–Warshall 算法
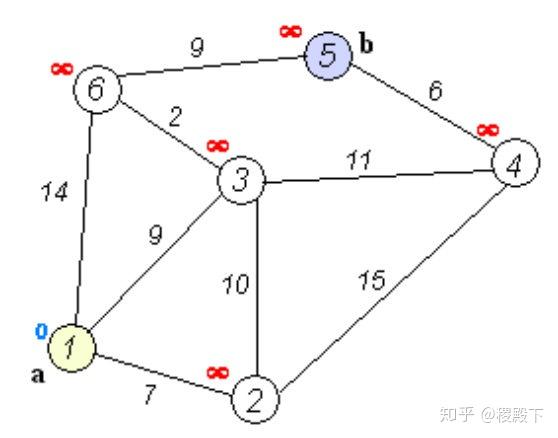
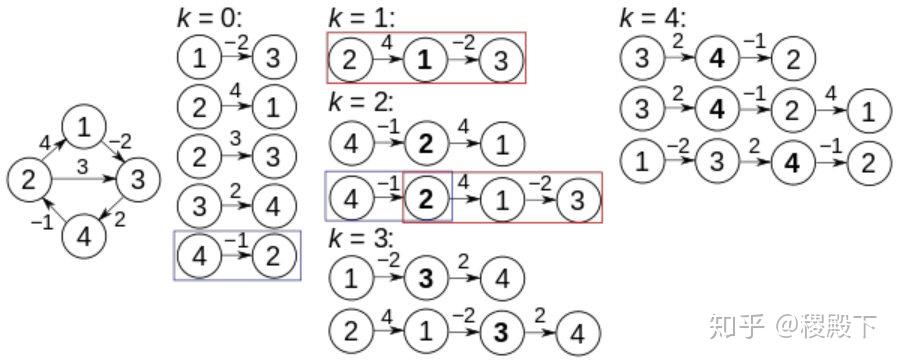
令  为中心矩阵(Centering Matrix),并定义平方距离矩阵
为中心矩阵(Centering Matrix),并定义平方距离矩阵

求矩阵  的特征值与特征向量(按特征值降序排列),
的特征值与特征向量(按特征值降序排列), 为第
为第  个特征值,
个特征值,  为对应的特征向量。则,降维矩阵为
为对应的特征向量。则,降维矩阵为

例如,原始数据如下:
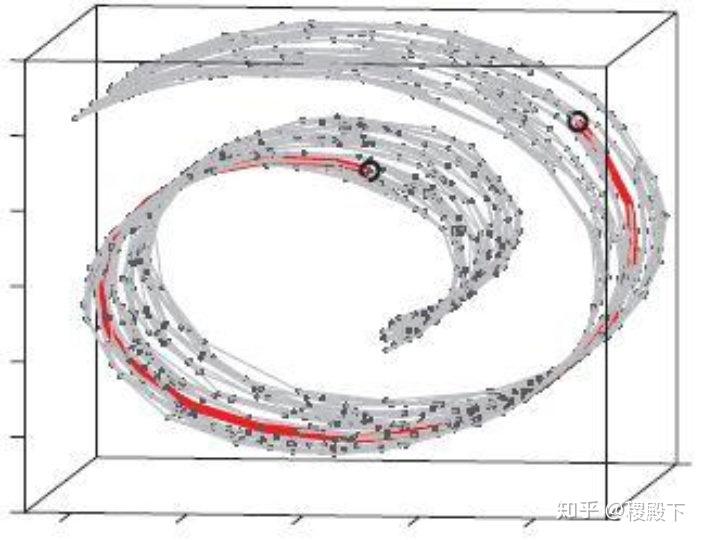
等距映射后的数据如下:
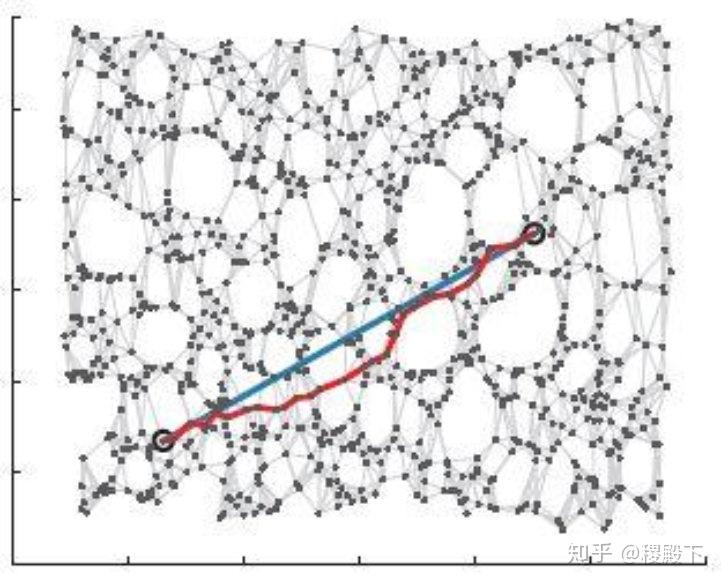
- 构造临近关系图:对每一个点,将它与指定半径邻域内所有点相连(或与指定个数最近邻相连)
- 计算最短路径:计算临近关系图所有点对之间的最短路径,得到距离矩阵
- 多尺度分析:将高维空间中的数据点投影到低维空间,使投影前后的距离矩阵相似度最大
- 优点:非线性、非迭代、全局最优、参数可调节
- 缺点:容易受噪声干扰、在大曲率区域存在短路现象、不适用于非凸参数空间、大样本训练速度慢
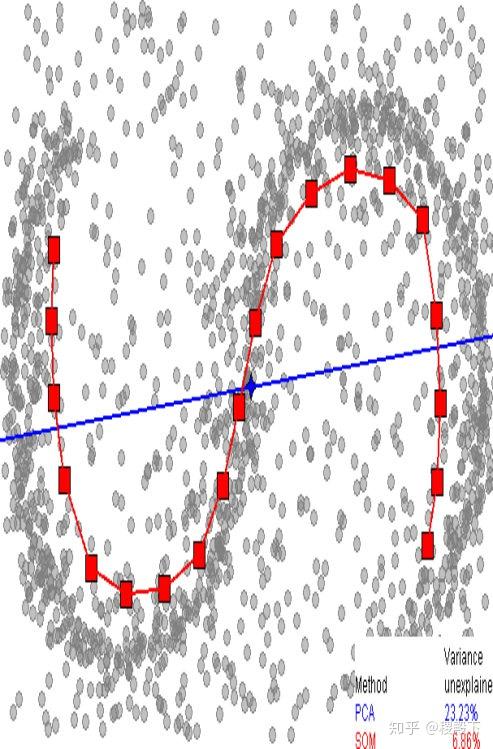
基本思想:保持数据点的原有流形结构
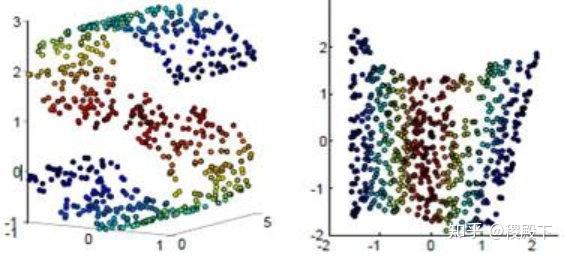
前提假设:采样数据所在的低维流形在局部是线性的,每个采样点可以用它的近邻点线性表示。 学习目标:在低维空间中保持每个邻域中的权值不变,即假设嵌入映射在局部是线性的条件下,最小化重构误差。
- 寻找每个样本点的
 近邻
近邻 
- 对每个点用
 个近邻进行重建,即求一组权值
个近邻进行重建,即求一组权值  ,满足
,满足  ,使得
,使得

- 求低维空间中的点集
 ,使得
,使得

- 计算权值,首先构造局部协方差矩阵


- 最小化
 https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+%5Cmin+%26%5Csum_i%7Cx_i-%5Csumj+w%7Bij%7Dx_%7Bij%7D%7C%5E2%5C%5C+%5Cmathrm%7Bs.t.%7D~~%26%5Csumjw%7Bij%7D+%3D1+%5Cend%7Baligned%7D+%5C%5C” alt=“\begin{aligned} \min
https://www.zhihu.com/equation?tex=%5Cbegin%7Baligned%7D+%5Cmin+%26%5Csum_i%7Cx_i-%5Csumj+w%7Bij%7Dx_%7Bij%7D%7C%5E2%5C%5C+%5Cmathrm%7Bs.t.%7D~~%26%5Csumjw%7Bij%7D+%3D1+%5Cend%7Baligned%7D+%5C%5C” alt=“\begin{aligned} \min &\sum_i|x_i-\sumj w{ij}x_{ij}|^2\ \mathrm{s.t.}&\sumjw{ij} =1 \end{aligned} \” eeimg=“1”/>
- 求得

- 计算低维数据

取  为
为  的最小
的最小  个非零特征值所对应的特征向量,最终的输出结果即为
个非零特征值所对应的特征向量,最终的输出结果即为 大小的矩阵。
大小的矩阵。
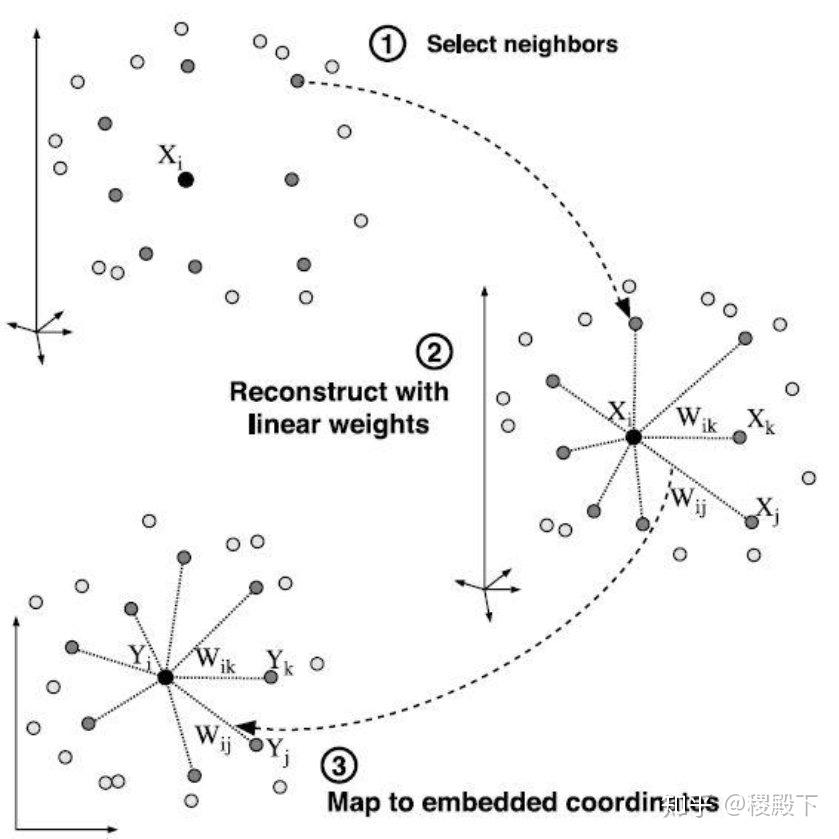
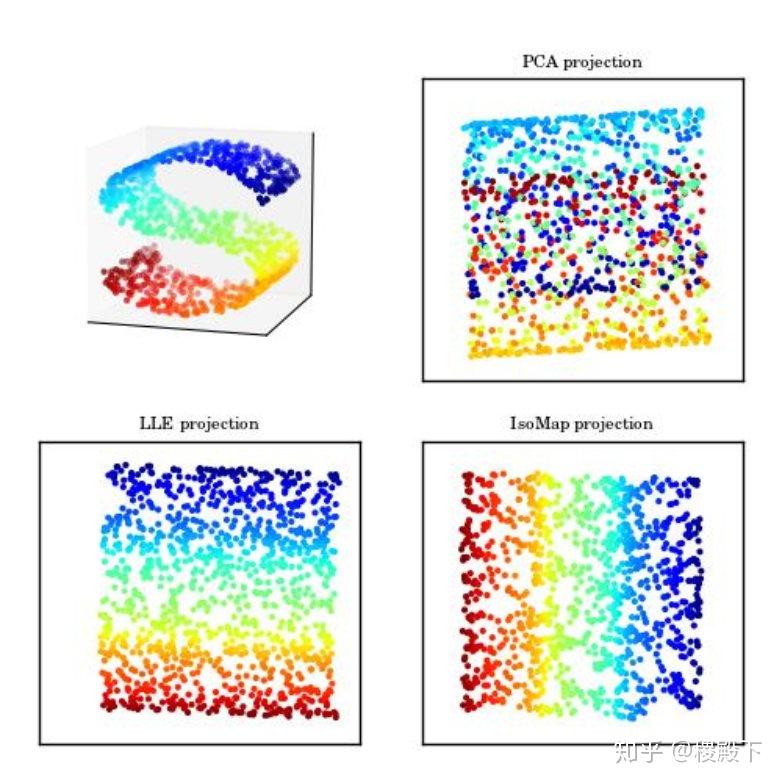
作者|Zolzaya Luvsandorj
编译|VK
来源|Towards Data Science
原文链接: https:// towardsdatascience.com/ introduction-to-nlp-part-5a-unsupervised-topic-model-in-python-733f76b3dc2d
这篇文章将向你展示一个构建基本无监督主题模型的简化示例。我们将使用潜Dirichlet分配(LDA)模型。简而言之,LDA是一个概率模型,其中每个主题被视为单词的混合,而每个文档被视为主题的混合。利用LDA,我们将尝试从语料库中识别潜在主题。

本文假设你能够访问并熟悉Python,包括安装包、定义函数和其他基本任务。如果你是Python新手,那么这是一个很好的开始。
◻️ 确保安装了numpy、pandaps、nltk、sklearn、matplotlib、seaborn、wordcloud和pyLDAvis;
◻️ 确保你已从nltk下载了“stopwords”和“wordnet”语料库。
下面的脚本可以帮助你下载这些语料库。
import nltk nltk.download(‘stopwords’) nltk.download(‘wordnet’) 让我们通过导入所需的包来准备环境。我们还将定义一组要忽略的停用词:
讯享网# 数据集 from sklearn.datasets import fetch_20newsgroups
数据操纵
import numpy as np import pandas as pd pd.options.display.max_colwidth = 100
文本预处理与建模
from nltk.tokenize import RegexpTokenizer from nltk import pos_tag from nltk.stem import WordNetLemmatizer from nltk.corpus import stopwords from sklearn.feature_extraction.text import ENGLISH_STOP_WORDS from sklearn.model_selection import train_test_split, GridSearchCV from sklearn.feature_extraction.text import CountVectorizer from sklearn.decomposition import LatentDirichletAllocation from sklearn.pipeline import Pipeline
可视化
import matplotlib.pyplot as plt import seaborn as sns sns.set(style=‘whitegrid’, context=‘talk’) from wordcloud import WordCloud import pyLDAvis import pyLDAvis.sklearn
警告
import warnings warnings.filterwarnings(‘ignore’, category=DeprecationWarning)
停用词
stop_words = set(ENGLISH_STOP_WORDS).union(stopwords.words(‘english’)) stop_words = stop_words.union([‘let’, ‘mayn’, ‘ought’, ‘oughtn’,
'shall']) print(f“Number of stop words: {len(stop_words)}”)
为了建立直觉,让我们用4个文档创建一个小示例。我们可以看到有两个主题:芒果和棋盘游戏。让我们用LDA来确定主题群:
讯享网data = [“We played board games yesterday.”,
"Delicious mango!", "She plays board games every weekend.", "Mangoes are now in season. Buy them while they are cheap."] example = pd.DataFrame({‘document’: data}) example
作为第一步,我们将使用词袋方法将文本数据转换为数字数据。进行此转换的最简单方法是使用sklearn中的CountVectorizer():
讯享网# 转换为文档-术语矩阵 vectoriser = CountVectorizer(stop_words=‘english’) example_matrix = vectoriser.fit_transform(example[‘document’])
提取特征/术语名称
feature_names = vectoriser.get_feature_names()
检查文档-术语矩阵
pd.DataFrame.sparse.from_spmatrix(example_matrix,
columns=feature_names)

如果我们能把“mango”和“mangoes”当作同一个词来处理,把“played”和“plays”当作相同的词来处理,那就更好了。为了解决这个问题,我们将创建一个自定义函数来预处理文本:
讯享网def preprocess_text(document):
"""将文档预处理为标准化标识.""" # 将单词标识成最小长度为3的字母标识 tokeniser = RegexpTokenizer(r'[A-Za-z]{3,}') tokens = tokeniser.tokenize(document) # 带词性标记的标签 pos_map = {'J': 'a', 'N': 'n', 'R': 'r', 'V': 'v'} pos_tags = pos_tag(tokens) # 小写和词根化 lemmatiser = WordNetLemmatizer() lemmas = [lemmatiser.lemmatize(t.lower(), pos=pos_map.get(p[0], 'v')) for t, p in pos_tags] # 删除停用词 keywords= [lemma for lemma in lemmas if lemma not in stop_words] return keywords 转换为文档-术语矩阵
vectoriser = CountVectorizer(analyzer=preprocess_text) example_matrix = vectoriser.fit_transform(example[‘document’])
提取特征/术语名称
feature_names = vectoriser.get_feature_names()
检查文档-术语矩阵
pd.DataFrame.sparse.from_spmatrix(example_matrix,
讯享网 columns=feature_names)
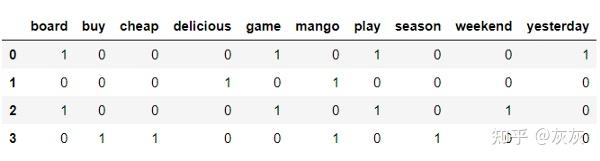
这看起来更好!如果你对我们刚刚做的预处理的细节不太清楚,这篇文章解释了预处理的基本步骤,并简要解释了词性标记和词义化:https://towardsdatascience.com/introduction-to-nlp-part-1-preprocessing-text-in-python-8f007d44ca96 。
好的,我们的数据处于模型可理解的状态,所以让我们构建一个简单的模型。
在构建模型时,我们需要为n_components参数定义主题的数量。在这个小例子中,我们知道阅读这四个简短的文档有两个主题。然而,通常你不知道主题的数量,而合适的主题数量则取决于你的判断。
# 建立lda模型 lda = LatentDirichletAllocation(n_components=2, random_state=0) lda.fit(example_matrix)检查主题
def describe_topics(lda, feature_names, top_n_words=5, show_weight=False):
讯享网"""打印lda模型中每个主题的前n个单词""" normalised_weights = lda.components_ / lda.components_.sum(axis=1)[:, np.newaxis] for i, weights in enumerate(normalised_weights): print(f" Topic {i+1} ") if show_weight: feature_weights = [*zip(np.round(weights, 4), feature_names)] feature_weights.sort(reverse=True) print(feature_weights[:top_n_words], '\n') else: top_words = [feature_names[i] for i in weights.argsort()[:-top_n_words-1:-1]] print(top_words, '\n')
describe_topics(lda, feature_names, show_weight=True)

主题1中最重要的单词是“mango”(权重为0.2266),而主题2中最重要的单词是“play”、“game”和“board”(每个单词的权重均为0.1919)。
现在让我们将每个主题的概率分配给文档:
example[[‘topic1’, ‘topic2’]] = lda.transform(example_matrix) example 
很好,现在我们将通过找到每个记录的概率最高的主题来确定主导主题:
讯享网example[‘top’] = example.iloc[:, 1:3].idxmax(axis=1) example[‘prop’] = example.iloc[:, 1:3].max(axis=1) example

我们让主题名称更具描述性:
topic_mapping = {‘topic1’: ‘mango’, ‘topic2’: ‘game’} example[‘topic’] = example[‘top’].map(topic_mapping) example 
太棒了,现在我们看看它如何为新文档分配主题:
讯享网def assign_topic(document):
"""使用lda模型预测为文档指定主题。""" tokens = vectoriser.transform(pd.Series(document)) probabilities = lda.transform(tokens) topic = probabilities.argmax() topic_name = topic_mapping['topic'+str(topic+1)] return topic_name assign_topic(“Board games are so fun!”)
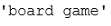
耶!它正确地预测了主题。 热身之后,我们来看一个更现实的例子。
在本节中,我们将使用新闻组数据集中的三个主题。这是为了使这篇介绍性文章的内容易于管理,更易于理解。
讯享网# 加载数据 categories = [‘comp.sys.mac.hardware’, ‘rec.sport.baseball’,
'alt.atheism'] newsgroups = fetch_20newsgroups(remove=(‘headers’, ‘footers’,
讯享网 'quotes'), categories=categories)
df = pd.DataFrame(newsgroups[‘data’], columns=[‘document’]) print(“Shape:”, df.shape) df.head()
快速检查一下是否有不具信息性的例子。查看文档的字符长度。
df[‘n_characters’] = df[‘document’].str.len() df.describe().T 
最小值为零-这些是空文档。让我们看看20个字符以下的文档是什么样子的:
讯享网df.query(“n_characters<20”).sort_values(‘n_characters’, ascending=False)
这些文件告诉我们的信息不多,所以我们把它们排除在外。但是如果你认为应该包括它们或者应该更改阈值,可以在以下脚本中进行调整:
df.query(“n_characters>=20”, inplace=True) df.nsmallest(5, ‘n_characters’) 
现在,数据集中最短的示例看起来更合理。
在没有监督的情况下,通常没有针对目标数据集进行划分检查。但是,我认为最好留出一些看不见的测试文档,以便稍后对模型进行测试。用下面的脚本,我们将为此保留5条记录。
讯享网X_train, X_test = train_test_split(df[‘document’], test_size=5,
random_state=1) print(“Train size:”, X_train.shape) print(“Test size:”, X_test.shape)

现在我们将训练文档矢量化(即转换为数值表示)。为了更实用,假设我们不知道主题的数量,我们将尝试使用网格搜索来找到合适数量的主题。
如果你对粗略的主题范围有一个直观的猜测,缩小选项范围的一个方法是运行网格搜索。但是,仅将网格搜索的输出作为指导,并检查主题是否有意义。
讯享网# 预处理文本 vectoriser = CountVectorizer(analyzer=preprocess_text, min_df=5) document_term_matrix = vectoriser.fit_transform(X_train)
跨所选参数运行网格搜索
lda = LatentDirichletAllocation(learning_method=‘online’, random_state=0) param_grid = {‘n_components’: [2, 3, 4, 5]} lda_search = GridSearchCV(lda, param_grid=param_grid, cv=3) lda_search.fit(document_term_matrix)
检查网格搜索输出
results = pd.DataFrame(lda_search.cvresults)
.sort_values("rank_test_score") results[[‘param_n_components’, “rank_test_score”, ‘mean_test_score’,
讯享网 'std_test_score']]
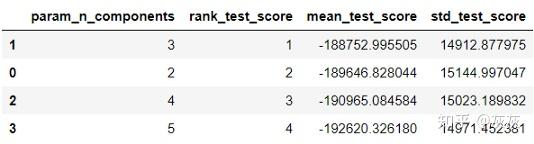
在这种情况下,score表示对数似然值,这个值越高越好。我们发现3个组分的平均测试分数最高。很好,我们知道从新闻组数据中提取了3个主题!我们运行一个包含3个主题的LDA模型,并将其与管道中的预处理步骤放在一起。
如果你不熟悉管道,这篇文章(滚动到1.Pipeline)用一个简单的例子解释了它的作用:https://towardsdatascience.com/pipeline-columntransformer-and-featureunion-explained-f5491f815f 。
n_components = 3 pipe = Pipeline([(‘vectoriser’, CountVectorizer(analyzer=preprocess_text, min_df=5)),讯享网 ('lda', LatentDirichletAllocation(n_components=n_components, learning_method='online', random_state=0))])
pipe.fit(X_train)
检查主题
feature_names = pipe[‘vectoriser’].get_feature_names() describe_topics(pipe[‘lda’], feature_names, top_n_words=10)

似乎第一个主题是关于宗教,第二个主题是关于体育,第三个主题是关于Mac/Apple的-但是我们需要更多的信息。我们将尝试在主题语境化部分更好地理解主题。
让我们将主题概率添加到每个训练文档中。
pd.options.display.max_colwidth = 50 train = pd.DataFrame(X_train) columns = [‘topic’+str(i+1) for i in range(n_components)] train[columns] = pipe.transform(X_train) train.head() 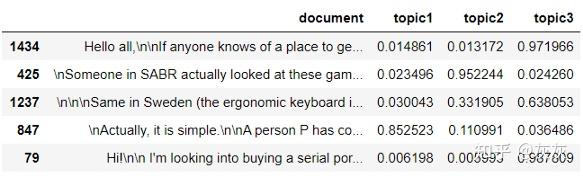
现在我们来组织概率。我们将创建几个新列:
讯享网train = train.assign(top1=np.nan, prob1=np.nan, top2=np.nan,
prob2=np.nan, top3=np.nan, prob3=np.nan) for record in train.index:
讯享网top = train.loc[record, 'topic1':'topic3'].astype(float).nlargest(3) train.loc[record, ['top1', 'top2', 'top3']] = top.index train.loc[record, ['prob1', 'prob2', 'prob3']] = top.values
train.drop(columns=“document”).head()
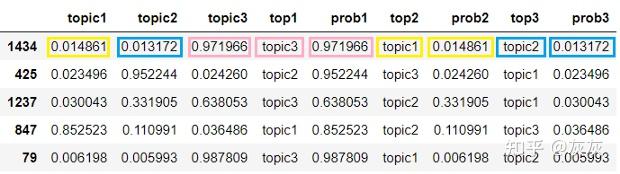
top1列存储每个记录的最主要主题,prob1列存储最主要主题的概率分数。top2和prob2在第二个最主要的主题上也是一样的,依此类推。我发现用这种方式组织可以更容易地进一步分析主题。让我们来检查一下两个主题的概率相同的情况。
train.loc[train[‘prob1’]==train[‘prob2’], ‘document’:‘topic3’] 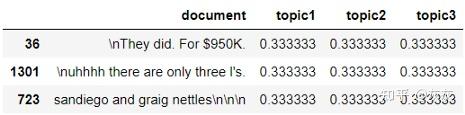
很难说这些文档有主导主题,因为这三个主题的概率都是相等的。由于这些文件相当短,所以模型给出的概率相等似乎是合理的。
幸运的是这种情况只有3个。如果我们对train[‘prob2’]==train[‘prob3’]重复相同的操作,将找到相同的3条记录。如果你好奇,可以通过调整上面的代码来查看。
现在我们可视化最主要的主题的概率分布。理想情况下,我们更希望大多数概率集中在更高的值上。
讯享网plt.figure(figsize=(12,5)) sns.kdeplot(data=train, x=‘prob1’, hue=‘top1’, shade=True,
common_norm=False) plt.title(“Probability of dominant topic colour coded by topics”);
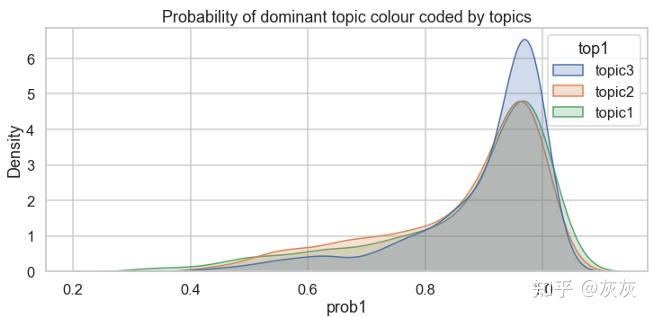
很高兴看到大多数值都接近1。让我们检查概率值的汇总统计:
讯享网train[[“prob1”, “prob2”, “prob3”]].describe()
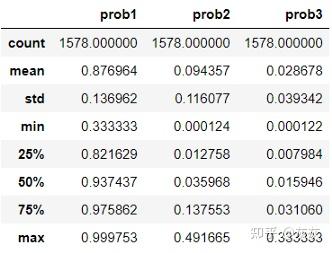
最主要主题的平均概率为0.9374。太棒了!
现在我们找出每个主题的最前面的单词来理解发现的主题:
def inspect_term_frequency(df, vectoriser, n=30):讯享网"""在语料库中显示前n个常用词""" document_term_matrix = vectoriser.transform(df) document_term_matrix_df = pd.DataFrame(document_term_matrix.toarray(), columns=feature_names) term_frequency = pd.DataFrame(document_term_matrix_df.sum(axis=0), columns=['frequency']) return term_frequency.nlargest(n, 'frequency')
fig, ax = plt.subplots(1, 3, figsize=(16,12)) for i in range(n_components):
topic = 'topic' + str(i+1) topic_df = train.loc[train['top1']==topic, 'document'] freqs = inspect_term_frequency(topic_df, pipe['vectoriser']) sns.barplot(data=freqs, x='frequency', y=freqs.index, ax=ax[i]) ax[i].set_title(f"Top words for {topic}") plt.tight_layout()
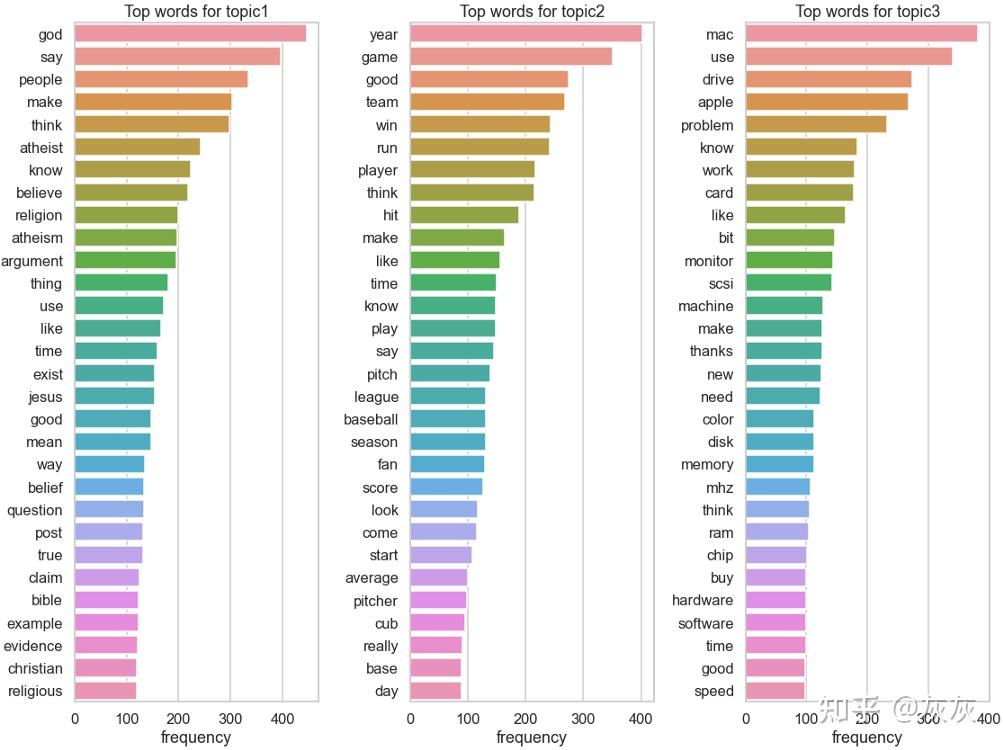
从我们目前所看到的情况来看,可以总结如下主题:
主题1:与宗教有关,尤其是无神论;
主题2:与运动有关,尤其是棒球;
主题3:电脑相关,尤其是Mac/Apple。
让我们看看每个主题的词云:
讯享网fig, ax = plt.subplots(1, 3, figsize=(20, 8)) for i in range(n_components):
topic = 'topic' + str(i+1) text = ' '.join(train.loc[train['top1']==topic, 'document'].values) wordcloud = WordCloud(width=1000, height=1000, random_state=1, background_color='Black', colormap='Set2', collocations=False, stopwords=stop_words).generate(text) ax[i].imshow(wordcloud) ax[i].set_title(topic) ax[i].axis("off");

我们还可以使用pyLDAvis包以交互方式可视化主题:
讯享网pyLDAvis.enable_notebook() pyLDAvis.sklearn.prepare(pipe[‘lda’],
pipe['vectoriser'].transform(X_train), pipe['vectoriser'])
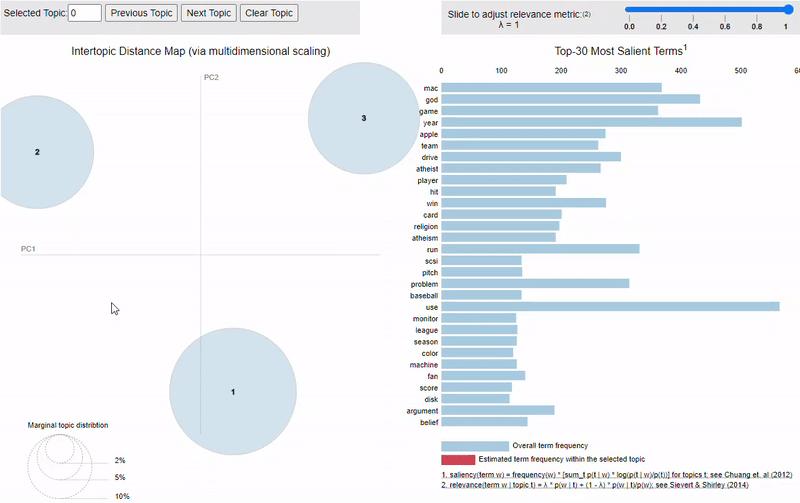
根据目前为止的主题探索,我们可以将主题命名如下:
讯享网topic_mapping = {‘topic1’: ‘atheism’,
'topic2': 'baseball', 'topic3': 'mac'} train[‘topic’] = train[‘top1’].map(topic_mapping) train[[‘document’, ‘topic’]].head()

对于这个特定的数据集,我们还可以将模型预测与数据集附带的标签进行比较。然而,目标标签通常不会像这样容易访问。
讯享网# 向数据框添加目标标签 target_mapping = dict(enumerate(newsgroups[‘target_names’])) df = pd.merge(df, pd.Series(newsgroups[‘target’], name=‘target’),
how='left', left_index=True, right_index=True) df[‘target’] = df[‘target’].map(target_mapping)
向训练添加目标标签
train = pd.merge(train, df[‘target’], how=‘left’, left_index=True,
讯享网 right_index=True)
train[[‘document’, ‘topic’, ‘target’]].head()

很高兴看到这些主题与这些示例相匹配。你可以进一步扩展检查(例如,查看混淆矩阵)。
让我们仔细看看几个训练示例,看看主题有多准确:
def assign_topic(document):讯享网"""使用lda模型预测为文档指定主题""" probabilities = pipe.transform(document) topic = probabilities.argmax() topic_name = topic_mapping['topic'+str(topic+1)] return topic_name
for i, document in enumerate(X_train.sample(3, random_state=2).values):
print(f" Test example {i+1} ") print(document, '\n') print(f"Assigned topic: {assign_topic(np.atleast_1d(document))}", '\n')

到目前为止,这三个例子看起来不错,但是如果你看更多的例子,可能会有一些没有意义的任务。现在让我们为新案例分配主题并检查:
讯享网for i, document in enumerate(X_test.values):
print(f" Test example {i+1} ") print(document, '\n') print(f"Assigned topic: {assign_topic(np.atleast_1d(document))}", '\n')


你同意这些任务吗?我们对照一下目标标签:
讯享网test = pd.DataFrame(X_test) test[columns] = pipe.transform(X_test) test[‘topic’] = test.loc[:, ‘topic1’:‘topic3’].idxmax(axis=1).map(topic_mapping) test = pd.merge(test, df[‘target’], how=‘left’, left_index=True,
right_index=True) test
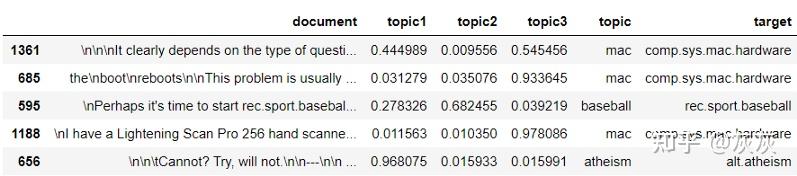
瞧,现在你知道如何运行一个基本的无监督主题模型了!
虽然我们在这篇文章中只运行了一次包含3个主题的迭代,但实际上你可能会发现自己使用不同的主题数和其他参数运行多个迭代来找到合适的模型。所以继续尝试吧!⭐️
如果你还没理清LDA (Linear Discriminant Analysis),那么接下来的几分钟就能掌握一个叫LDA的机器学习新乐子
一句话:一种线性的、基于分类的、监督学习的数据降维工具,相应地可以得到特征提取方法。
当然这些词换一下就是别的算法了,比如二次的、基于回归的、无监督的,猜猜分别都是些啥?
简而言之,LDA将数据从m维特征空间线性投影到n维(小于m维)特征空间,核心就是找这么一个线性投影P。
目标是使得投影后的同类数据之间的差距尽可能小,不同类数据之间的差距尽可能大。这里是两个目标,会用除法将其整合为一个目标。
投影降维后的投影点就是经过特征提取后的点,那么降维的过程就是针对分类的特征提取过程。
话术都具备了,接下来就是用数学来描述上面的文字了。
数学建模就是用数学语言来描述咱们的想法、限制和目的,对于上面的所谓原理,其实有各种各样的数学实现方式,其中一种,就是Fisher的数学建模:
Fisher, R. A.[1] (1936). “The Use of Multiple Measurements in Taxonomic Problems”
当然,原版是个二分类的,这里直接上多分类的威力加强版
Rao, R. C.[2] (1948). “The utilization of multiple measurements in problems of biological classification”. Journal of the Royal Statistical Society, Series B.
下面开始写公式了,假设有一堆数据 , 以及对应的指标集
, 以及对应的指标集 ,
,  的每一行就是一个数据点,
的每一行就是一个数据点, 的对应位置是其标签,
的对应位置是其标签, 的每一列表示了所有数据的同一特征。
的每一列表示了所有数据的同一特征。
 分类数据会将其投影到至多
分类数据会将其投影到至多 维空间中,比如二分类问题可以投影到直线上,三分类问题可以投影到平面上。。先别急为何至多是
维空间中,比如二分类问题可以投影到直线上,三分类问题可以投影到平面上。。先别急为何至多是 维,后面会有一个解释。
维,后面会有一个解释。
上面提到了,有两个需要量化表征的指标,下面来一步步建立表征
设![P=[p_1,p_2,\cdots, p_{k-1}]](https://51itzy.com/uploads/202412/23/d8d6e00325d3a7fb.jpg) 是
是 个投影坐标轴的方向。
个投影坐标轴的方向。
假设所有属于 类的数据是
类的数据是 ,记
,记 类的均值为
类的均值为

同种数据的分离散度可以用下面公式表示(形似协方差估计):

同种数据经过投影后的分离散度可以用下面公式表示:

所有的分离散度之和为

然后考虑不同种类之间的差距,记 为所有
为所有 的平均值,那么种类之间的分离度由下面式子表示:
的平均值,那么种类之间的分离度由下面式子表示:

其投影的分散度为

然后考虑 应该取多少?为了达成上一节的既定目标,定义一个除法颇为合理,最大化Between差异/Within差异,即
应该取多少?为了达成上一节的既定目标,定义一个除法颇为合理,最大化Between差异/Within差异,即

取好了一个特征方向,然后选取第二个, ,为了提取与
,为了提取与 不相干的特征,选择正交方向
不相干的特征,选择正交方向

这里的正交是在 导出內积的意义下,即
导出內积的意义下,即 ,如果觉得这个正交很诡异的话,可以在下一小节找到一些合理性。同理,一直做到第
,如果觉得这个正交很诡异的话,可以在下一小节找到一些合理性。同理,一直做到第 个,目标为
个,目标为

以上就是表世界的所有相关数学原理(数学的里世界有概率解释,暂跳过)
那么怎么求解呢?好巧不巧,上面的 刚好是
刚好是 的最大的
的最大的 个特征值对应的特征向量。
个特征值对应的特征向量。
当然, 的求逆特别危险,比如
的求逆特别危险,比如 是奇异的,那么上面的分式表达中的分母就可以无限趋近于0了,因此通常会加上一个正则化因子替代上方的所有计算:
是奇异的,那么上面的分式表达中的分母就可以无限趋近于0了,因此通常会加上一个正则化因子替代上方的所有计算:

从这里也可以看到为何最多做到 维的投影了,因为
维的投影了,因为 最大秩为
最大秩为 。往后的特征值为0,对应特征向量就没有显著意义了。
。往后的特征值为0,对应特征向量就没有显著意义了。
矩阵的特征值想必大家都知道的,形如:

如果S是对称非负定的话,那么PCA的各个主特征方向就是S的特征。 S的各个特征向量可以大致由以下过程获得:

而对于方程

就是所谓的广义特征值及其特征向量了,当 时,蜕化为上面的方程。假设
时,蜕化为上面的方程。假设 对称正定的,做个代换
对称正定的,做个代换 ,进而变成了原来的问题:
,进而变成了原来的问题:

如果 是对称非负定的,那么
是对称非负定的,那么 也是对称非负定的,进而其各个特征向量可以由下面的式子给出
也是对称非负定的,进而其各个特征向量可以由下面的式子给出

做个代换其实又回到了LDA的熟悉配方:

其中的正交关系的话,就是

也就是咱们上一节中提到的那个有点诡异的正交关系的根源。
PCA是无监督方法,LDA是有监督方法,这是最大的区别。
要硬说联系也挺紧密,都是基于方差的降维方法。并且,在LDA的所有点都是各自单独类的特殊情形下,仅极大化类间差距的时候,PCA跟LDA在算法上就是一模一样的。还有一个东西稍微少见一些,叫Partial Least Square (PLS),偏最小二乘法,也是数据与矩阵的玩具,下次再说吧
在这个例子中,制造一堆13维特征的数据,为什么是十三维?随便选的而已,随个别的也行,构造如下:
讯享网np.random.seed(103)
X1 = np.random.randn(100, 13) * 0.3 + np.random.rand(13)
Y1 = np.ones(100)
X2 = np.random.randn(100, 13) 0.2 + np.random.rand(13)
Y2 = np.ones(100) 2
X3 = np.random.randn(100, 13) 0.5 + np.random.rand(13)
Y3 = np.ones(100) 3
X = np.concatenate([X1, X2, X3])
Y = np.concatenate([Y1, Y2, Y3])
先看几个图
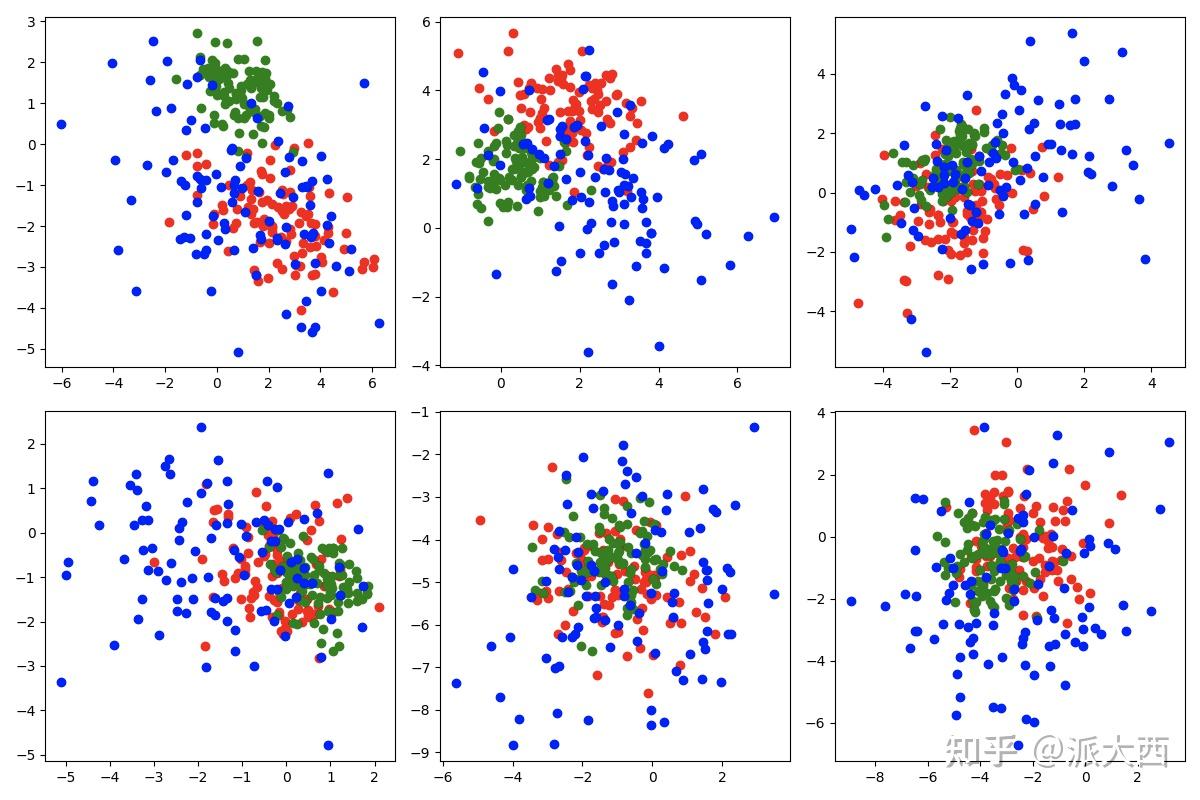
但是如果我们变化一下投影的角度,就能得到挺好的降维,变化效果如图
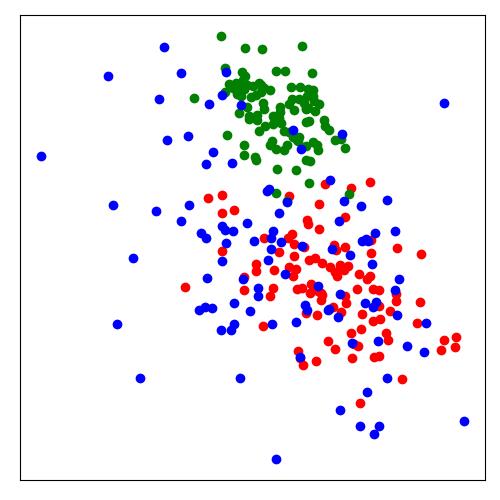
结果是这个,非常像魏蜀吴三国的地图(挑了一下种子)
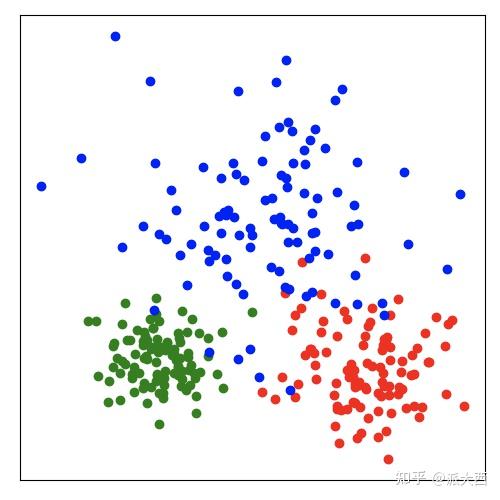
算法和作图的代码:
import numpy as np
import matplotlib.pyplot as plt
class LDA:
讯享网<span class="k">def</span> <span class="nf">__init__</span><span class="p">(</span><span class="bp">self</span><span class="p">,</span> <span class="n">n_components</span><span class="o">=</span><span class="kc">None</span><span class="p">):</span> <span class="bp">self</span><span class="o">.</span><span class="n">n_components</span> <span class="o">=</span> <span class="n">n_components</span> <span class="bp">self</span><span class="o">.</span><span class="n">eig_vectors</span> <span class="o">=</span> <span class="kc">None</span> def fit(self, X: np.ndarray, y: np.ndarray):
<span class="n">m</span><span class="p">,</span> <span class="n">n</span> <span class="o">=</span> <span class="n">X</span><span class="o">.</span><span class="n">shape</span> <span class="n">classes</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">unique</span><span class="p">(</span><span class="n">y</span><span class="p">)</span> <span class="n">K</span> <span class="o">=</span> <span class="nb">len</span><span class="p">(</span><span class="n">classes</span><span class="p">)</span> <span class="n">S_tatol</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">cov</span><span class="p">(</span><span class="n">X</span><span class="o">.</span><span class="n">T</span><span class="p">)</span> <span class="o">*</span> <span class="p">(</span><span class="n">m</span> <span class="o">-</span> <span class="mi">1</span><span class="p">)</span> <span class="n">SW</span> <span class="o">=</span> <span class="nb">sum</span><span class="p">([</span><span class="n">np</span><span class="o">.</span><span class="n">cov</span><span class="p">(</span><span class="n">X</span><span class="p">[</span><span class="n">y</span> <span class="o">==</span> <span class="n">classes</span><span class="p">[</span><span class="n">i</span><span class="p">]]</span><span class="o">.</span><span class="n">T</span><span class="p">)</span> <span class="o">*</span> <span class="p">(</span><span class="n">np</span><span class="o">.</span><span class="n">count_nonzero</span><span class="p">(</span><span class="n">y</span> <span class="o">==</span> <span class="n">classes</span><span class="p">[</span><span class="n">i</span><span class="p">])</span> <span class="o">-</span> <span class="mi">1</span><span class="p">)</span> <span class="k">for</span> <span class="n">i</span> <span class="ow">in</span> <span class="nb">range</span><span class="p">(</span><span class="n">K</span><span class="p">)])</span> <span class="n">SB</span> <span class="o">=</span> <span class="n">S_tatol</span> <span class="o">-</span> <span class="n">SW</span> <span class="bp">self</span><span class="o">.</span><span class="n">eig_vectors</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">linalg</span><span class="o">.</span><span class="n">eigh</span><span class="p">(</span><span class="n">np</span><span class="o">.</span><span class="n">linalg</span><span class="o">.</span><span class="n">pinv</span><span class="p">(</span><span class="n">SW</span><span class="p">)</span> <span class="o">@</span> <span class="n">SB</span><span class="p">)[</span><span class="mi">1</span><span class="p">][:,</span> <span class="p">::</span><span class="o">-</span><span class="mi">1</span><span class="p">]</span> <span class="k">def</span> <span class="nf">transform</span><span class="p">(</span><span class="bp">self</span><span class="p">,</span> <span class="n">X</span><span class="p">,</span> <span class="n">y</span><span class="o">=</span><span class="kc">None</span><span class="p">,</span> <span class="n">ax</span><span class="o">=</span><span class="kc">None</span><span class="p">):</span> <span class="k">assert</span> <span class="n">X</span> <span class="ow">is</span> <span class="ow">not</span> <span class="kc">None</span><span class="p">,</span> <span class="s2">"Fit the LDA model first!"</span> pc = X.dot(self.eig_vectors[:, :self.n_components])
讯享网 <span class="k">if</span> <span class="bp">self</span><span class="o">.</span><span class="n">n_components</span> <span class="o">==</span> <span class="mi">2</span> <span class="ow">and</span> <span class="n">ax</span> <span class="ow">is</span> <span class="ow">not</span> <span class="kc">None</span><span class="p">:</span> <span class="k">if</span> <span class="n">y</span> <span class="ow">is</span> <span class="kc">None</span><span class="p">:</span> <span class="n">ax</span><span class="o">.</span><span class="n">scatter</span><span class="p">(</span><span class="n">pc</span><span class="p">[:,</span> <span class="mi">0</span><span class="p">],</span> <span class="n">pc</span><span class="p">[:,</span> <span class="mi">1</span><span class="p">])</span> <span class="k">else</span><span class="p">:</span> <span class="n">colors</span> <span class="o">=</span> <span class="p">[</span><span class="s1">'r'</span><span class="p">,</span> <span class="s1">'g'</span><span class="p">,</span> <span class="s1">'b'</span><span class="p">]</span> <span class="n">labels</span> <span class="o">=</span> <span class="n">np</span><span class="o">.</span><span class="n">unique</span><span class="p">(</span><span class="n">y</span><span class="p">)</span> <span class="k">for</span> <span class="n">color</span><span class="p">,</span> <span class="n">label</span> <span class="ow">in</span> <span class="nb">zip</span><span class="p">(</span><span class="n">colors</span><span class="p">,</span> <span class="n">labels</span><span class="p">):</span> <span class="n">class_data</span> <span class="o">=</span> <span class="n">pc</span><span class="p">[</span><span class="n">y</span> <span class="o">==</span> <span class="n">label</span><span class="p">]</span> <span class="n">ax</span><span class="o">.</span><span class="n">scatter</span><span class="p">(</span><span class="n">class_data</span><span class="p">[:,</span> <span class="mi">0</span><span class="p">],</span> <span class="n">class_data</span><span class="p">[:,</span> <span class="mi">1</span><span class="p">],</span> <span class="n">c</span><span class="o">=</span><span class="n">color</span><span class="p">)</span> <span class="k">return</span> <span class="n">pc</span> fig, ax = plt.subplots(1, 1, figsize=(5, 5))
# ax = ax.ravel() fig.set_tight_layout(True)
lda = LDA(n_components=2)
lda.fit(X, Y)
target_p = lda.eig_vectors
P = np.random.randn(2, 13)
lda.transform(X, Y, ax)
plt.show()
 在这个深度学习降维抽特征霸占视野的年代,咱们还能在这篇传统文章的文末相会,真是种缘分~ 不妨点赞关注 @派大西,他长期致力于输出干货与乐子
在这个深度学习降维抽特征霸占视野的年代,咱们还能在这篇传统文章的文末相会,真是种缘分~ 不妨点赞关注 @派大西,他长期致力于输出干货与乐子
参考链接:
- https://en.wikipedia.org/wiki/Linear_discriminant_analysis
- https://www.slideshare.net/engalaatharwat/lda-classifier-tutorial
- https://machinelearningmastery.com/linear-discriminant-analysis-for-machine-learning/
- https://www.section.io/engineering-education/linear-discriminant-analysis/
作者|Sejal Dua
编译|VK
来源|Towards Data Science
原文链接: https:// towardsdatascience.com/ nlp-preprocessing-and-latent-dirichlet-allocation-lda-topic-modeling-with-gensim-713d516c6c7d
在我的上一篇文章中,我介绍了如何从电子邮件中提取元数据。
具体地说,我演示了如何使用Gmail API收集标题、副标题、作者、出版物和分钟数(以阅读时间估算文章长度)。
有了这些数据,我的目标是调查:1)媒体的推荐引擎是如何很好地了解我的阅读兴趣的,2)我的兴趣是如何随着时间的推移而演变的。
那么它是如何工作的呢?通过检测单词频率和单词之间的距离等模式,主题模型根据最常出现的单词和表达式对相似的文档进行聚类。通过这些信息,你可以快速推断哪些文本与你感兴趣的主题相关。
主题可以定义为“语料库中共现单词的重复模式”。一个好的主题模型可能会推断“健康”、“医生”、“患者”、“医院”等词都属于“医疗保健”范畴。“神经网络”、“反向传播”和“损失”等词可能被指定为“深度学习”主题栏。
然而,需要注意的是,由于主题模型是一种无监督的方法,模型可以了解到某些单词相互关联,以了解“健康”、“医生”、“患者”、“医院”作为已知类别与“医疗保健”如何关联。
相反,用户可以从类似文档的未标记分组中获得见解,也可以在包含分类主题标签的文本上训练主题分类模型(如果需要这些标签作为输出)。
有许多技术方法可用于执行主题模型。其中包括潜Dirichlet分配(LDA)、TextRank、潜在语义分析(LSA)、非负矩阵分解(NMF)、Pachinko分配模型(PAM)等。
在本文中,我们将重点介绍如何实现最常用的LDA方法。
LDA是一种使用变分异常最大化(VEM)算法开发的矩阵分解技术。LDA建立在这样一个前提之上:每个文档都可以用主题的概率分布来描述,每个主题都可以用单词的概率分布来描述。这可以让我们更清楚地了解主题之间的联系。
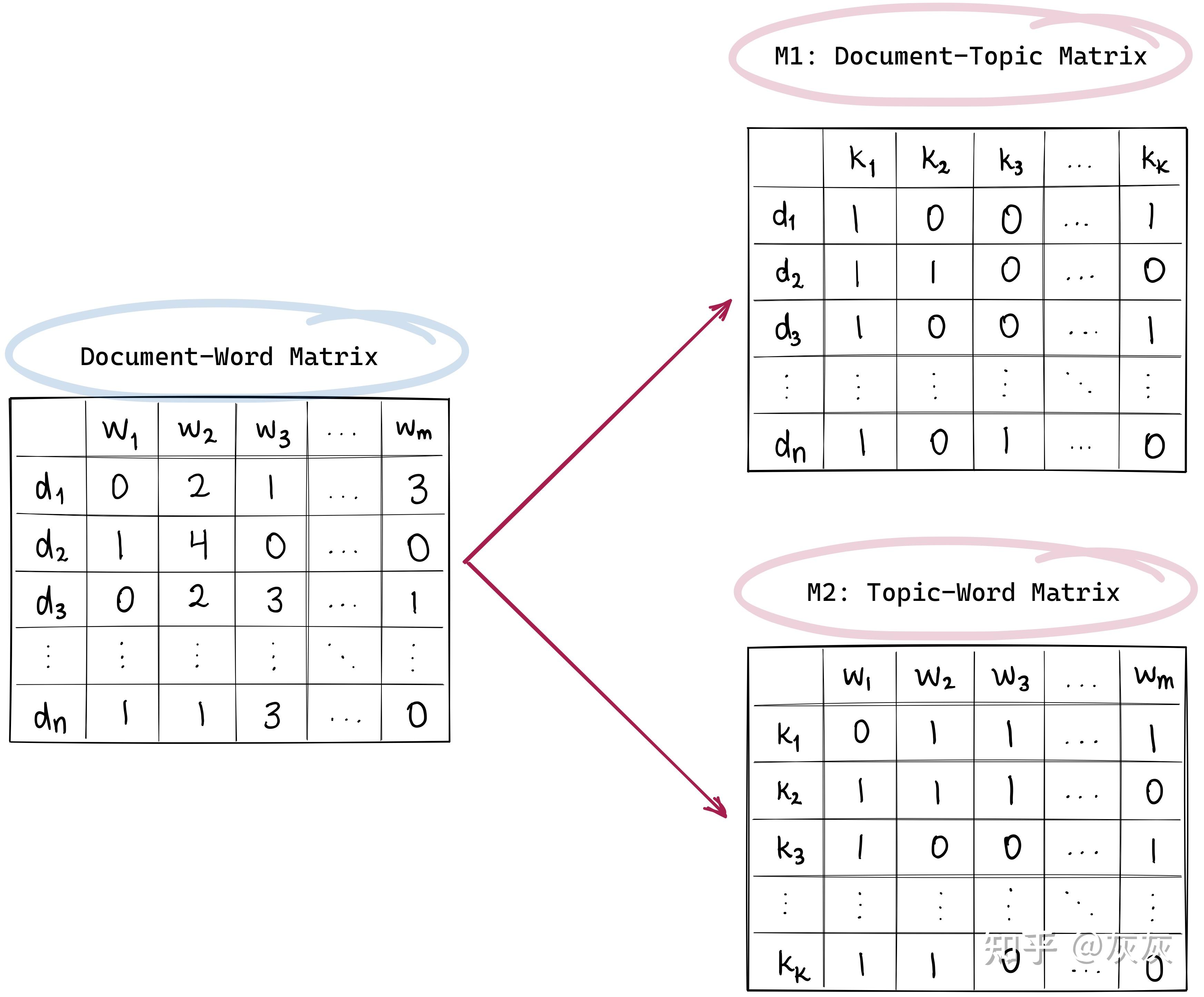
在向量空间中,任何语料库或文档集合都可以表示为由N个文档和M个单词组成的文档单词矩阵。
该矩阵中每个单元格的值表示文档D_i中单词W_j的频率。LDA算法通过将文档词矩阵转换为两个低维矩阵M1和M2来训练主题模型,这两个矩阵分别表示文档主题和主题词矩阵。
我们只需导入一个方便的Python包,创建一个LDA对象,到此为止-试着理解LDA依赖于贝叶斯理论和两个关键概率计算来更新属于主题t的给定单词w的概率:
- p(主题t |文档d)-文档d中指定主题t的概率
- p(单词w |主题t)-在主题t中单词w的数量
从本系列的第1部分中,我们可以获得下面的数据集。删除重复项后,剩下7.1k行。
在开始任何主题模型之前,让我们确保安装并导入所有需要的库。
# 重要 import base64 import re from tqdm import tqdm import numpy as np import pandas as pd import matplotlib.pyplot as plt import datapane as dp dp.login(token=‘INSERT_TOKEN_HERE’)Gensim 和 LDA
import gensim import gensim.corpora as corpora from gensim.utils import simple_preprocess from gensim.models import CoherenceModel from gensim.parsing.preprocessing import STOPWORDS import pyLDAvis import pyLDAvis.gensim # 不要跳过这个
NLP 相关
import contractions import demoji import string import nltk from nltk.stem import WordNetLemmatizer, SnowballStemmer from nltk.stem.porter import * from nltk.corpus import stopwords stop_words = stopwords.words(‘english’) nltk.download(‘wordnet’) import spacy
绘图工具
from bokeh.plotting import figure, output_file, show from bokeh.models import Label from bokeh.io import output_notebook import matplotlib.colors as mcolors import matplotlib.pyplot as plt %matplotlib inline
杂项
from sklearn.manifold import TSNE from pprint import pprint
任何NLP相关项目中最关键的步骤之一是对所有文档进行逐列预处理。
虽然有一些标准的清理方法,一般来说,可以应用于任何语料库,但也有相当数量的直觉驱动的决策,我们必须作出。
例如,它对表情符号有意义吗?停用词呢?数字应该保持原样、转换成文本还是完全删除?是否应忽略或调查所有文档中80%以上的单词?同一个词根的变体应该词干化还是词形还原?
讯享网def preprocess(text_col):
""" 这个函数将在pandas系列(如df['text'])上应用NLP预处理lambda函数。 这些函数包括将文本转换为小写,删除表情符号,扩展缩写,删除标点符号, 去掉数字,去掉停顿词,语义化等等。
讯享网""" # 转换为小写 text_col = text_col.apply(lambda x: ' '.join([w.lower() for w in x.split()])) # 删除emojis text_col = text_col.apply(lambda x: demoji.replace(x, "")) # 展开缩写 text_col = text_col.apply(lambda x: ' '.join([contractions.fix(word) for word in x.split()])) # 删除标点符号 text_col = text_col.apply(lambda x: ''.join([i for i in x if i not in string.punctuation])) # 删除数字 text_col = text_col.apply(lambda x: ' '.join(re.sub("[^a-zA-Z]+", " ", x).split())) # 删除停用词 stopwords = [sw for sw in nltk.corpus.stopwords.words('english') if sw not in ['not', 'no']] text_col = text_col.apply(lambda x: ' '.join([w for w in x.split() if w not in stopwords])) # 词形还原 text_col = text_col.apply(lambda x: ' '.join([WordNetLemmatizer().lemmatize(w) for w in x.split()])) # 删除短单词 text_col = text_col.apply(lambda x: ' '.join([w.strip() for w in x.split() if len(w.strip()) >= 3])) return text_col 上面的函数将pandas series对象作为输入,并应用lambda函数,这些函数将文本转换为小写、删除表情、展开缩写、删除标点符号、删除停用词、执行词形还原以及删除太短(长度小于3个字符)的词。
当涉及到停用词删除时,许多人认为这是一个实用的预处理步骤,总是利大于弊。
但是,我强烈建议你实际打印出你决定使用的任何停用词列表(注意:我使用*nltk.corpus.stopwords.words(‘english’)*集),并进行上下文感知调整以优化你的语料库。
一个常见的例子,一个停用词,需要一点慎重考虑后才能删除“not”。当文本数据源包含来自用户的基于意见的评论或其他详细描述时,删除“not”往往会混淆数据中的主要信号源。
在这里,我们只看媒体文章的标题和副标题,所以我们是否保留“not”并不重要,但我会原则上保留它。
对于那些不熟悉词形还原和词干化的人来说,你可以把词形还原看作是将单词还原为原本词形的过程——例如,第三人称的单词变成第一人称,过去和将来时态的动词变成现在时。
词干是通过去掉后缀或前缀,将单词的词形变化减少到词根形式的过程。与词干分析不同,词形还原确保根单词或词形是属于英语的有效单词。
例如,runs、running和ran都将映射到词形run。为了说明词形还原和词干化的区别,单词intelligence 和intelligent的词干是intellig,实际上它不是一个有效的英语单词。
n-gram是给定文本或文档样本中n个项的连续序列。Bigrams是文档中经常同时出现的两个词(例如data_science, machine_learning, sentiment_analysis)。Trigrams是经常出现的三个词(例如,towards_data_science, natural_language_processing, exploratory_data_analysis)
Gensim的短语模型可以构建和实现bigram、trigram、quadram等等。短语的两个重要参数是minu count和threshold。这些参数的值越高,单词就越难被组合成bigram和trigram。
gensim Python库使创建LDA主题模型变得非常简单。我们唯一要做的准备工作就是创建一本词典和语料库。
字典是单词ID到单词的映射。要创建字典,可以创建内置的gensim.corpora.dictionary对象。
从这里开始,filter_extremes方法是必不可少的,以确保我们在字典中获得所需的单词频率和表示形式。
id2word = corpora.Dictionary(data_preprocessed) id2word.filter_extremes(no_below=15, no_above=0.4, keep_n=80000) filter_extremes方法采用3个参数。让我们来分析一下它们的含义:
- 筛选出出现在少于15个文档中的单词
- 过滤掉出现在超过40%文档中的单词
- 在以上两个步骤之后,只保留前80000个最频繁的单词
语料库本质上是单词ID到单词频率的映射。对于每个文档,将创建一个单词包表示:
讯享网corpus = [id2word.doc2bow(text) for text in texts]
使用字典和语料库,我们可以获得一个示例文档的可读词频映射:
[[(‘better’, 1), (‘creating’, 1), (‘data_visualization’, 1), (‘design’, 1), (‘principle’, 1), (‘towards’, 1)]] 非常整洁…还要注意我们的一个Bigram(数据可视化)是如何出现的!
构建LDA模型的代码仅一行代码。
讯享网lda_model = gensim.models.ldamodel.LdaModel(corpus=corpus,
id2word=id2word, num_topics=10, random_state=100, update_every=1, chunksize=100, passes=10, alpha='auto', per_word_topics=True) 我们已经介绍了语料库和词典参数。我们将首先将num_topics固定为10个。random_state对模型没有很大影响;它只是用来获得不会随笔记本每次执行而改变的结果。update_every确定应更新模型参数的频率。chunksize是每个训练区块中要使用的文档数。Pass是一次训练的总数。最后一个参数per_word_topics设置为True时,计算主题列表,按每个单词最可能主题的降序排序,以及它们的phi值乘以特征长度(即字数)。
现在我们有了“经过训练的”主题模型(记住:这是一种无监督的方法……把它想象成簇,而不是其他任何东西),让我们打印10个主题中的前10个关键词。

有趣的是,python显然是这个语料库中的一个流行关键词,这是理所当然的!看起来我们有一个关于学习好的设计的主题,一个关于涉及twitter数据的机器学习文章(也许?),如何在研究中取得成功,生产力等。这是一个好的开始,但它还没有为我们提供一个令人满意的整体画面。
你可能会问的下一个问题是,仅仅从构建模型的一行代码,我们如何知道我们的模型到底有多好?
主题模型领域通常使用两种评估指标:困惑度和一致性。
- “困惑”捕获了模型对以前从未见过的新数据的惊讶程度。
- 连贯性衡量主题中得分较高的词之间的语义相似度。
要计算这些值,只需执行以下代码:
讯享网from gensim.models import CoherenceModel
计算困惑度 (分数越低越好)
print(‘Perplexity: ’, round(lda_model.log_perplexity(corpus), 2))
计算连贯性 (分数越高越好)
coherence_model_lda = CoherenceModel(model=lda_model, texts=data_preprocessed, dictionary=id2word, coherence=‘c_v’) coherence_lda = coherence_model_lda.get_coherence() print(‘Coherence Score: ’, round(coherence_lda, 2))
我们的LDA模型的初始困惑度和一致性分别为-6.68和0.4。展望未来,我们将希望尽量减少困惑,最大限度地提高连贯性。
现在你可能想知道,除了打印关键词或者wordcloud之外,我们如何能够可视化我们的主题。
幸运的是我们得到了pyLDAvis!pyLDAvis是一个用于交互式主题模型可视化的Python库。只需一小段代码,我们就可以获得这些交互式子图,这些子图描绘了2D平面上的主题与主题中前30个最相关和最显著的单词之间的距离(这两个指标都在下面可视化的右下角进行了数学定义)。
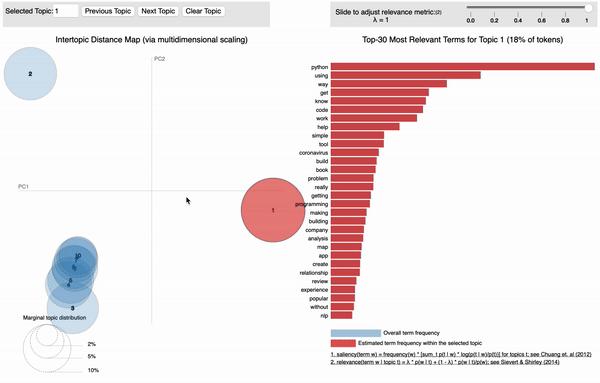
从上面的GIF可以明显看出,主题1和主题2彼此之间的距离最大,其余8个主题通常彼此相似。
虽然这是一种非常巧妙的可视化方法,有助于理解哪些主题关系最密切,哪些词语传递的信号最强,但目前的模型似乎并不十分聪明。换句话说,将鼠标悬停在每个主题上并不能完全帮助我们理解语料库中表示的所有主题。这是一个指标,我们可能要尝试更复杂的LDA模型。
MALLET由Andrew McCallum编写,是一个基于Java的包,用于统计自然语言处理、文档分类、聚类、主题模型、信息提取和其他文本机器学习应用。
mallet 主题模型工具包包含基于采样的LDA的高效实现。主要的优化差异在于Gensim LDA使用了变分Bayes采样方法,该方法比Mallet的Gibbs采样更快,但精度更低。
在我们开始使用Gensim之前,我们必须在系统上下载mallet-2.0.8.zip包并解压缩它。可在此处找到要下载的软件包和更详细的说明。安装并解压缩后,将mallet_path变量设置为下载当前驻留在本地计算机上的文件路径。一旦完成,我们就可以建立我们的LDA Mallet模型了!
Python为LDA提供Gensim包装。该包装的语法是gensim.models.wrappers.LdaMallet。该模块允许从训练语料库中估计LDA模型,并推断新的、看不见的文档上的主题分布。
mallet_path = ‘~/Downloads/mallet-2.0.8/bin/mallet’ # 更新路径 ldamallet = gensim.models.wrappers.LdaMallet(mallet_path,讯享网 corpus=corpus, num_topics=10, id2word=id2word, random_seed=42, workers=6)
最初,我们可以将主题数量设置为10。从我们的LdaMallet模型中不可能得到困惑分数,但可以得到一致性分数。下面是一些预览主题和计算连贯性分数的代码:
# 显示主题 pprint(ldamallet.show_topics(formatted=False)[:3])计算一致性评分
coherence_model_ldamallet = CoherenceModel(model=ldamallet, texts=data_preprocessed, dictionary=id2word, coherence=‘c_v’) coherence_ldamallet = coherence_model_ldamallet.get_coherence()
print(‘Coherence Score: ’, round(coherenceldamallet, 2)) data-pid=“ku6jiLj”>接下来,让我们以编程方式确定将文档划分到的主题的**数量。为了辨别这个数字,我们需要测试一些主题数量不断增加的模型,然后寻找产生足够高一致性值的最少主题数量。
讯享网def compute_coherence_values(dictionary, corpus, texts, limit, start=2, step=3): """ 计算c_v相干度为不同数量的主题 Parameters: ---------- dictionary : Gensim字典 corpus : Gensim语料库 texts : 输入文本的列表 limit : 主题的最大数目 Returns: ------- model_list : LDA主题模型列表 coherence_values : LDA模型相对应的相关值,对应于相应的主题数量 """ coherence_values = [] model_list = [] for num_topics in range(start, limit, step): model = gensim.models.wrappers.LdaMallet(mallet_path, corpus=corpus, num_topics=num_topics, id2word=id2word) model_list.append(model) coherencemodel = CoherenceModel(model=model, texts=texts, dictionary=dictionary, coherence='c_v') coherence_values.append(coherencemodel.get_coherence()) return model_list, coherence_values
注意:可能需要很长时间运行…
model_list, coherence_values = compute_coherence_values(dictionary=id2word, 讯享网 corpus=corpus, texts=data_preprocessed, start=8, limit=40, step=4)

从上面的图表中,我们可以看到我们的连贯性得分上升到0.38左右,然后上升到0.43左右,然后上升到0.45左右。用户可以选择一些他们认为合适的主题。接下来,我将在x=24个主题上选择第二个“拐点”,对应于约0.43的一致性分数。
我们可以像以前一样预览我们的主题,但我们也可以直接切入主题并进行讨论。为了实现这一点,我们实际上还需要执行一个额外的步骤:使用我们的Mallet模型的学习参数创建一个常规的LDA模型,以便我们可以将常规gensim LDA对象传递到pyLDAvis中。
这可以通过一个简单的函数来完成
上面的距离图比我们初始模型的图更有趣!我们可以看到更多关于二维平面的主题。特别是,有2-3组主题值得分析。
不考虑可视化中随机分配的主题标签,左下象限中的3个主题似乎主要由属于Python教程、指南和介绍的中等文章组成。右上角的两个主题的特点是其技术性较低的关键词,似乎更倾向于商业、营销和设计趋势和技能。右下角的主题似乎与构建可视化和以数据为中心的web应用程序有关。
从这里,我们可以为每篇文章的标题和副标题找到最主要的主题,我们还可以得到文档由主要主题表示的程度。这些新属性包含在以下数据表中:
通过获取每个主题的文档数、关键字和最具代表性的文档,我们还可以更好地了解每个主题。
# 在每个主题下分组最具代表性的文件 topic_df = pd.DataFrame() sent_topics_outdf_grpd = ldamallet_df[[‘Dominant_Topic’, ‘Topic_Rep’, ‘text’]].groupby(‘Dominant_Topic’) for i, grp in sent_topics_outdf_grpd: 讯享网topic_df = pd.concat([topic_df, grp.sort_values(['Topic_Rep'], ascending=[0]).head(1)], axis=0)
重置索引和重命名
topic_df.reset_index(drop=True, inplace=True) topic_df[‘Dominant_Topic’] = topic_df[‘Dominant_Topic’].astype(int) topic_df.rename(columns={‘Dominant_Topic’: ‘Topic_Num’, ‘text’: ‘Representative_Doc’}, inplace=True) 获取主题关键词
def get_keywords(topic_num): wp = optimal_model.show_topic(topic_num) topic_keywords = ", ".join([word for word, prop in wp]) return topic_keywords
topic_df[‘Keywords’] = topic_df[‘Topic_Num’].apply(lambda x: get_keywords(x)) 每个主题的文档数量
num_documents = pd.DataFrame(ldamallet_df[‘Dominant_Topic’].value_counts())
num_documents.reset_index(inplace=True) num_documents.columns = [‘Dominant_Topic’, ‘Num_Documents’]
合并
topic_df = num_documents.merge(topic_df, left_on=‘Dominant_Topic’, right_on=‘Topic_Num’, how=‘left’).drop(columns=[‘Dominant_Topic’]) topic_df = topic_df[[‘Topic_Num’, ‘Num_Documents’, ‘Keywords’, ‘Representative_Doc’, ‘Topic_Rep’]] topic_df上面提供了将主题信息的数据帧与这些关键属性相结合的代码。请注意,持续重置索引非常重要,以确保各列按照适当的主题编号对齐。这里可以利用pandas DataFrame的合并方法。
从上面包含描述每个主题的函数的表中,我们可以了解到主题0包含的文章最多。包含第二多文档的主题是令人遗憾的,但也是相当直观的,这些文章谈论“大流行”、“新冠病毒”和/或“冠状病毒”。
在项目的这一点上,我们已经形成了一个函数充分的主题模型,该模型利用数据源以一种合理的方式对文档进行聚类或分离,我们通过检查关键字、主题间距离和代表性文档来验证这一点。
使用特定于主题的词云作为进一步总结每个主题的手段可能会变得非常诱人,但我想说明的是,需要一种更好的可视化技术。

…如果出于某种原因,你仍然倾向于wordclouds,也许我们至少可以达成一个共识,即随着主题数量的增加,对wordclouds的视觉检查变得越来越重要。
所以,如果你准备从wordclouds毕业,牵着我的手,跟我来。让我们找到一种更好的可视化技术。
t-分布随机邻域嵌入(t-SNE)是由Laurens van der Maaten开发的一种非线性降维技术,特别适合于高维数据集的可视化。它广泛应用于图像处理、自然语言处理、基因组数据和语音处理。
那么它是如何工作的,我们为什么要使用它呢?简单地说,根据一个非常有用的介绍,t-SNE最小化了两种分布之间的差异:一种是测量输入对象的成对相似性的分布,另一种是测量嵌入中相应低维点的成对相似性的分布。通过这种方式,t-SNE将多维数据映射到低维空间,并尝试通过基于具有多个特征的数据点的相似性识别观察到的聚类来发现数据中的模式。
使用我们的24主题的Mallet模型,我们可以看到主题如何聚集。表示单个文章的每个圆圈的大小由主题表示百分比编码。因此,较大的圆圈与它们所属的主题联系更紧密——这些较大圆圈的簇很容易被识别为相关文章,它们可能共享一个连贯的主题。我们还可以将鼠标悬停在每个圆圈上,查看文章标题、副标题和主题表示百分比。
这种方法的一个缺点是,执行此过程后,输入特征不再可识别。因此,它主要是一种数据探索和可视化技术。此外,如果不花大量时间在圆圈上徘徊,或者不了解主题编号到关键字的映射,就很难从t-SNE散点图中获得对主题的一目了然的理解。
我希望通过这篇全面的教程,你能了解到一些关于Gensim主题模型的知识。所有代码都可以在下面链接的GitHub存储库中找到。
https://github.com/sejaldua/digesting-the-digest
参考引用
- https://towardsdatascience.com/latent-dirichlet-allocation-lda-9d1cd064ffa2
- https://www.machinelearningplus.com/nlp/topic-modeling-gensim-python/
- http://mallet.cs.umass.edu/
- https://towardsdatascience.com/basic-nlp-on-the-texts-of-harry-potter-topic-modeling-with-latent-dirichlet-allocation-f3c00f77b0f5
- https://towardsdatascience.com/mapping-the-tech-world-with-t-sne-7be8e

产后奶牛皱胃左移位(Left displaced abomasum , LDA)对畜牧业造成了巨大的经济损失。患有LDA的奶牛会经历过度的脂质动员和胰岛素抵抗。这种现象与肠道失调有关,但对肠道菌群在LDA异常代谢过程中发挥的作用知之甚少。
2022年10月,四川农业大学动物医学院曹随忠教授与左之才教授课题组在Microbiology Spectrum(IF 9.043)杂志上共同发表题为“Altered Fecal Microbiome and Correlations of the Metabolome with Plasma Metabolites in Dairy Cows with Left Displaced Abomasum”的研究文章。本研究通过联合肠道微生物16S rDNA测序和非靶向代谢组学技术,利用多组学数据分析了LDA奶牛肠道微生物及其代谢物与表型之间的相关性,阐明肠道微生物可能通过调节氨基酸组成参与脂肪分解和胰岛素抵抗的调控。中科新生命为本研究提供了16s测序和代谢组学的技术支持。

研究材料
LDA奶牛(n=10)和健康奶牛(n=10);血液和粪便样本
技术路线
步骤1:健康奶牛与LDA奶牛粪便样本16S rDNA测序;
步骤2:对所采集粪便样本进行非靶代谢组学分析;
步骤3:微生物组、粪便代谢组、血浆代谢组数据整合分析;
步骤4:对血浆样本进行靶向代谢氨基酸分析;
步骤5:结合健康奶牛与LDA奶牛血浆靶向氨基酸分析,构建代谢物-代谢物和代谢物-基因相互作用网络。
研究结果
1. LDA奶牛粪便微生物群改变
研究者先通过对健康奶牛和LDA奶牛粪便的16S rDNA测序分析鉴定其肠道微生物多样性的变化情况。结果表明肠道菌群丰富度因LDA事件而增加,同时LDA组与健康组的粪便微生物群落明显分离,群落异质性结构显著。
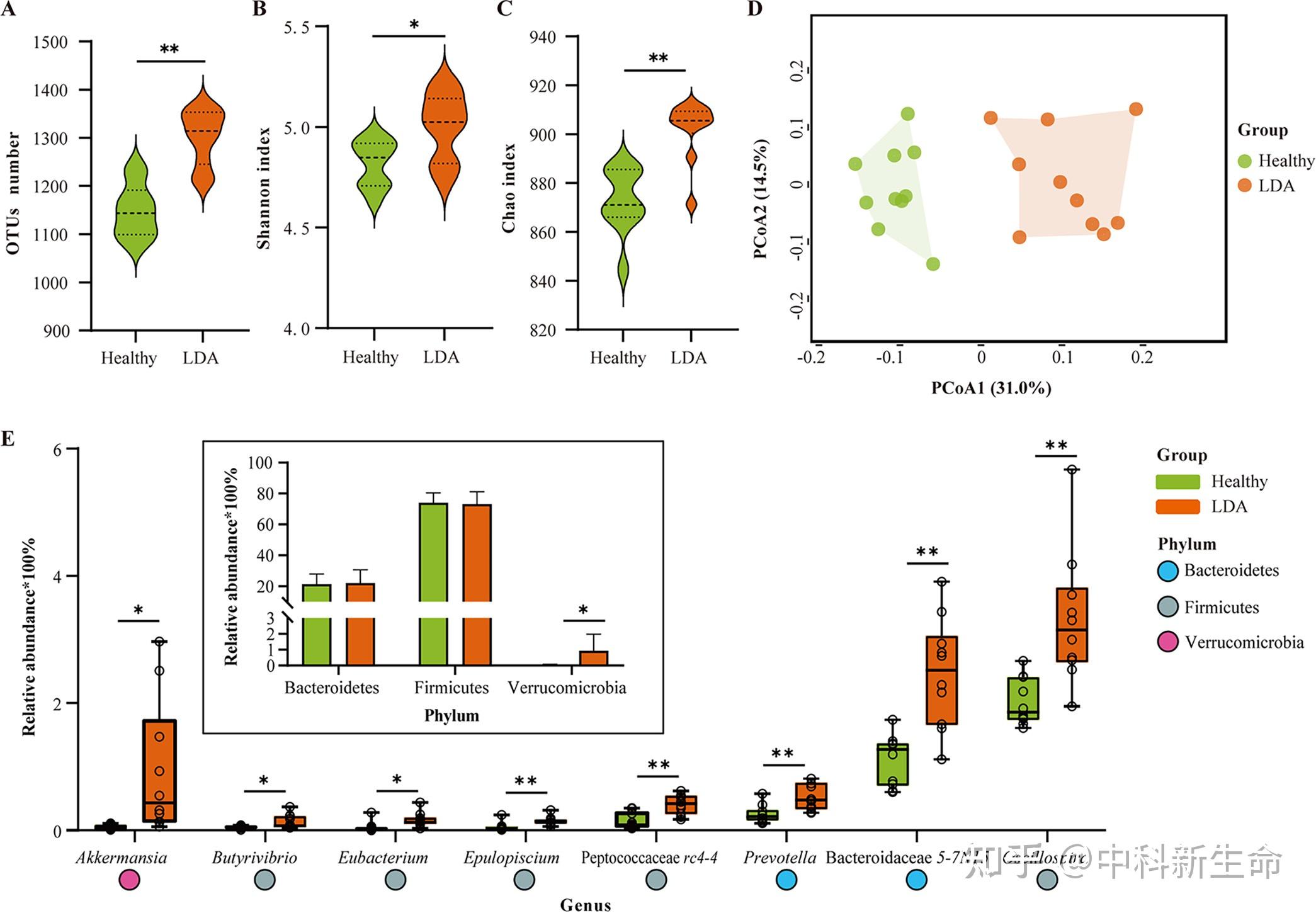
2. LDA对奶牛粪便代谢的影响
研究者对健康奶牛和LDA奶牛粪便进行非靶代谢组分析。在健康组和LDA组之间,共有48种代谢物存在差异,其中20种增加,28种降低。这些代谢产物分为脂类(37.50%)、核苷和核苷酸(14.58%)、有机酸(10.42%)、有机杂环化合物(20.83%)和苯类(8.33%)。
此外,粪便中鉴定出的20种差异代谢物来自宿主和肠道菌群之间的共同代谢过程。KEGG代谢通路分析显示,微生物群之间和与宿主共代谢之间享有两条共同通路:嘌呤代谢和卟啉-叶绿素代谢通路。
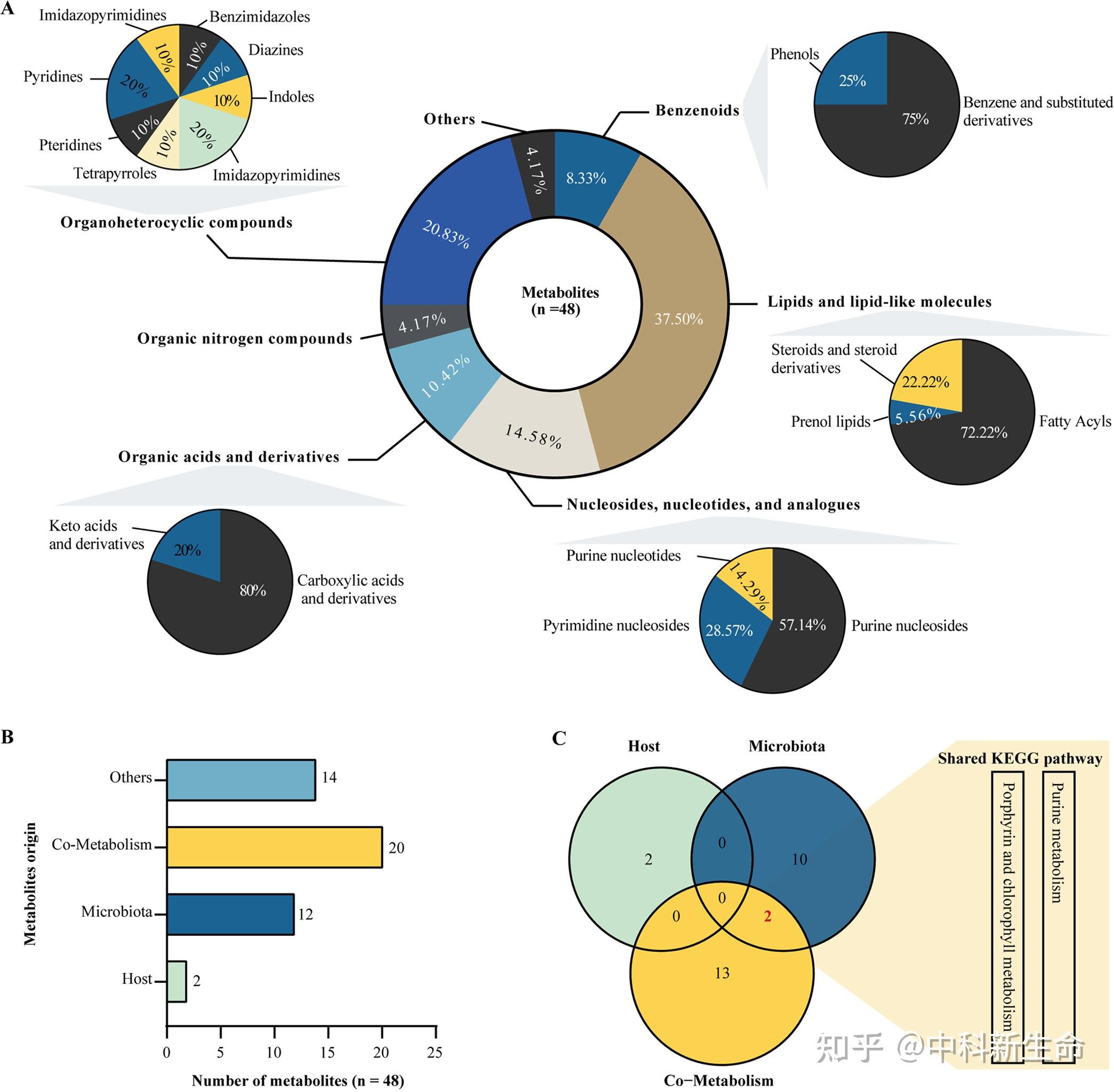
3. LDA中代谢物与粪便微生物群的关系
为了确定与LDA相关的代谢产物和肠道微生物群变化之间的相关性,研究者进行了Spearman相关性分析。Akkermansia、Oscillospira和Peptococcaceae rc4-4的丰度与粪便中鉴定出的大部分代谢物具有很强的相关性。研究者进一步将前期工作中所获得血浆代谢物数据与粪便代谢物数据整合分析,在粪便和血浆样本中筛选了8种共同的代谢物。结果显示:与健康奶牛相比,LDA组共代谢的胞苷和4-吡哆酸水平下降。LDA发生期间,奶牛体内微生物产生的水杨酸水平显著降低。LDA组粪便中亚油酸和硬脂酰肉碱含量低于健康组。LDA组血浆亚油酸和硬脂酰肉碱水平显著升高。
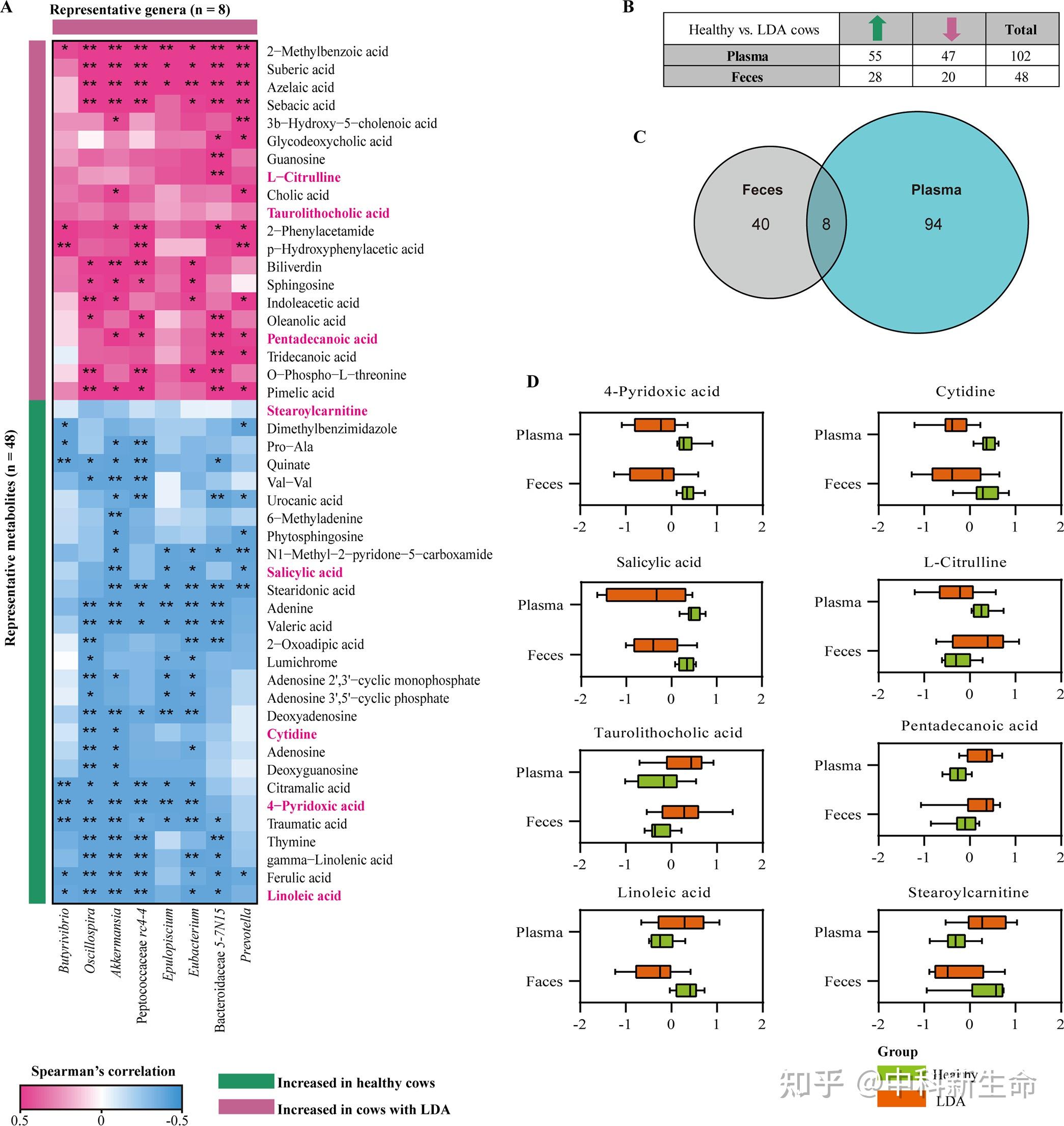
4. 组学数据和临床参数之间的关联
研究者检测发现LDA组和健康组之间的临床标志物存在显著差异,包括血清中NEFA、BHBA、葡萄糖、胰岛素、胆固醇、丙氨酸转氨酶、总胆红素、游离钙、氯和钾水平等。通过Spearman相关性分析研究肠道菌群、代谢物和临床标志物之间的关系,研究者观察到NEFA、BHBA和RQUICKI是与LDA事件相关的关键变量,进一步通过多元逻辑回归与ROC分析发现4-吡哆酸、水杨酸和胞苷可作为LDA特异性生物标志物。
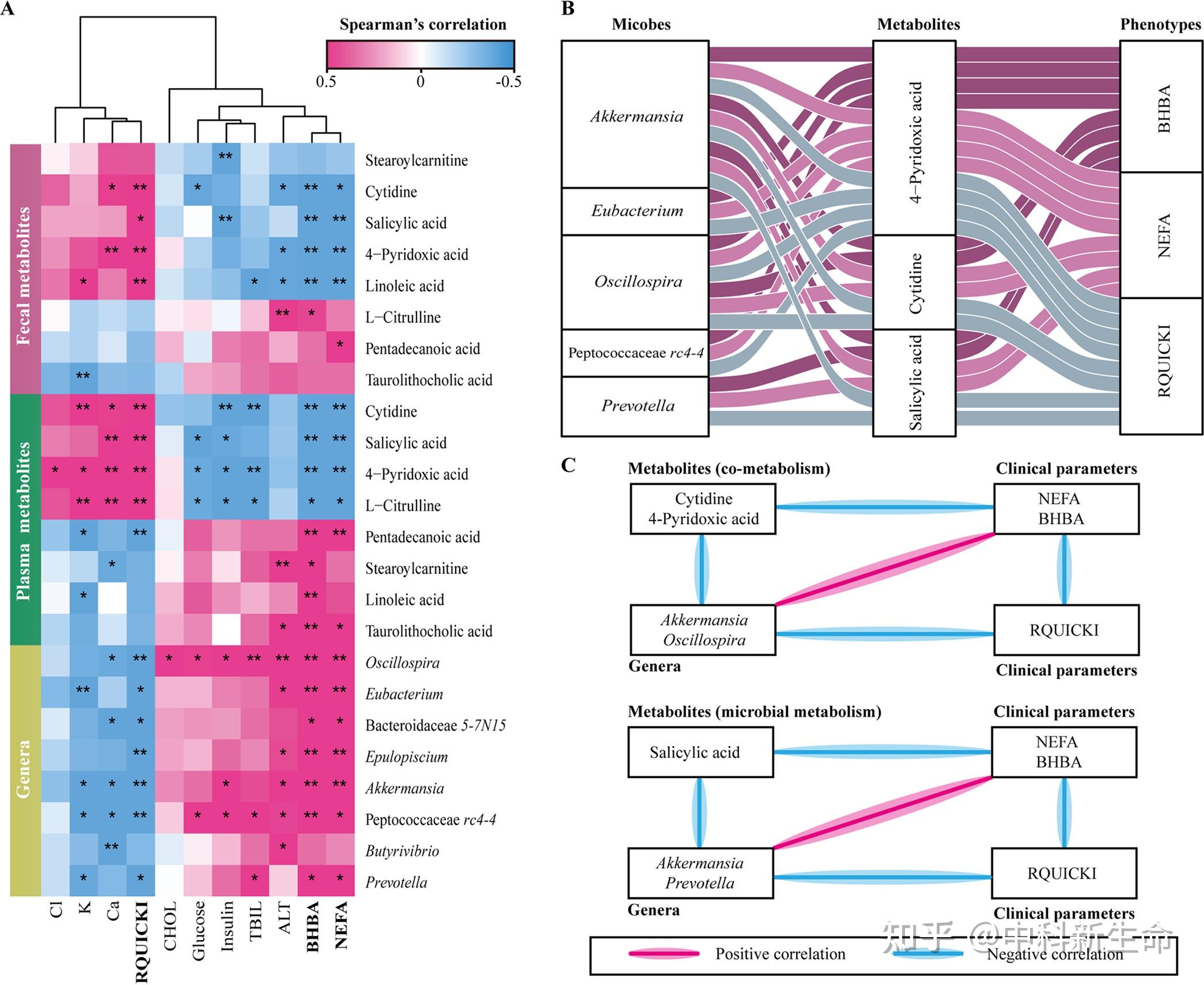
5. LDA奶牛血浆氨基酸的改变
研究者通过靶向代谢组学对奶牛血浆氨基酸进行了分析。结果显示,与健康组相比,LDA组血浆总氨基酸水平显著降低;同时LDA组BCAA(包括亮氨酸和异亮氨酸)的丰度显著增加,酪氨酸、色氨酸和组氨酸的丰度显著降低。相关性分析显示,循环总氨基酸水平的降低与微生物丰度的增加呈极显著负相关,与粪便和血浆中关键代谢物4-吡哆酸、胞苷和水杨酸的丰度则呈显著正相关。
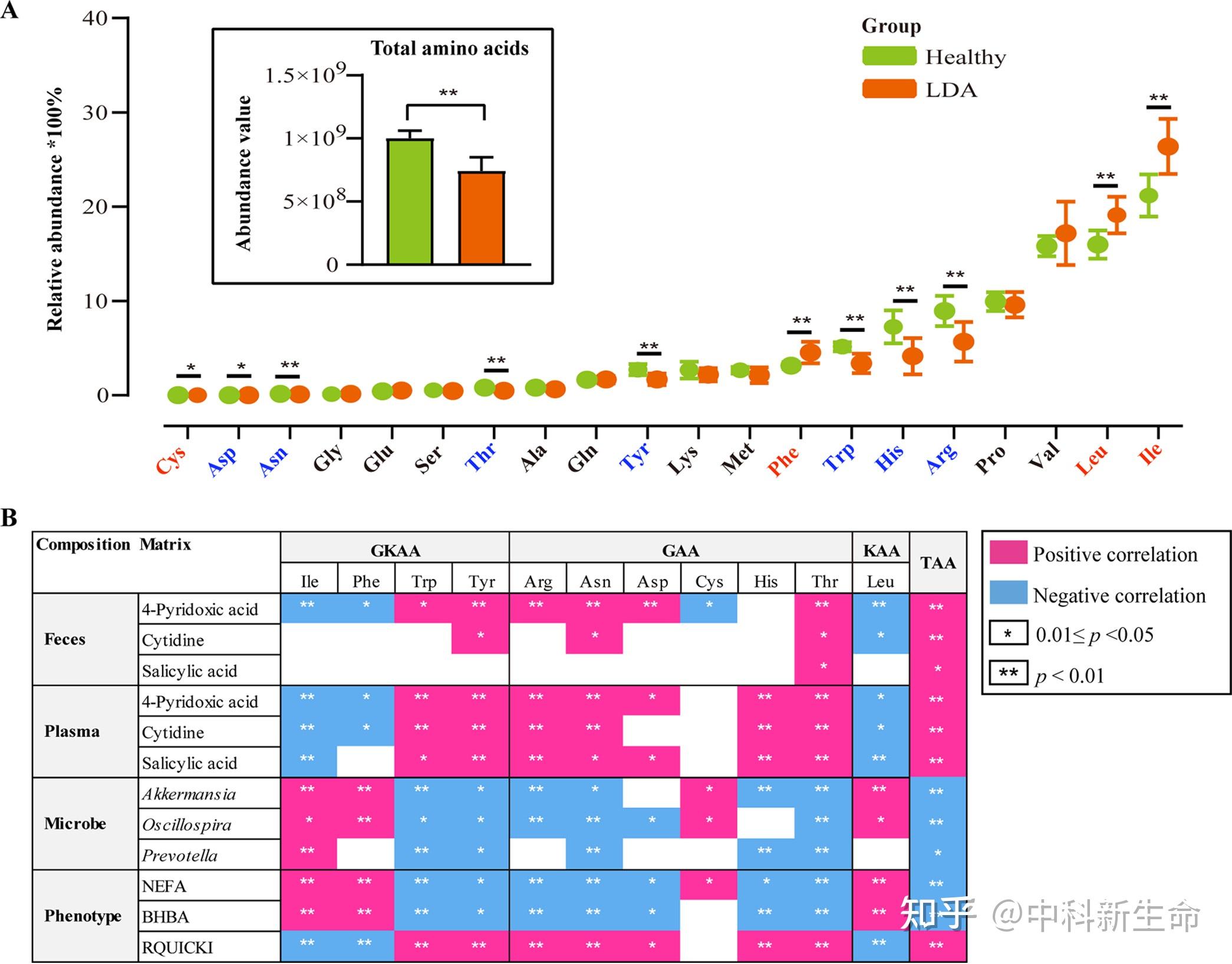
6. LDA的代谢途径和网络
研究者在粪便样品中鉴定出3697个KEGG同源物,其中203种在LDA和健康奶牛之间存在丰度差异。通过相关性分析,研究者发现亮氨酸和异亮氨酸的相对丰度与NEFA和BHBA的浓度有很强的相关性,表明LDA事件中生酮氨基酸代谢增加,糖酵解/糖异生和柠檬酸循环发生下调。通过构建代谢物-代谢物和代谢物-基因相互作用网络后进一步发现,肠道微生物产生的酶编码基因介导了这些生酮关系。
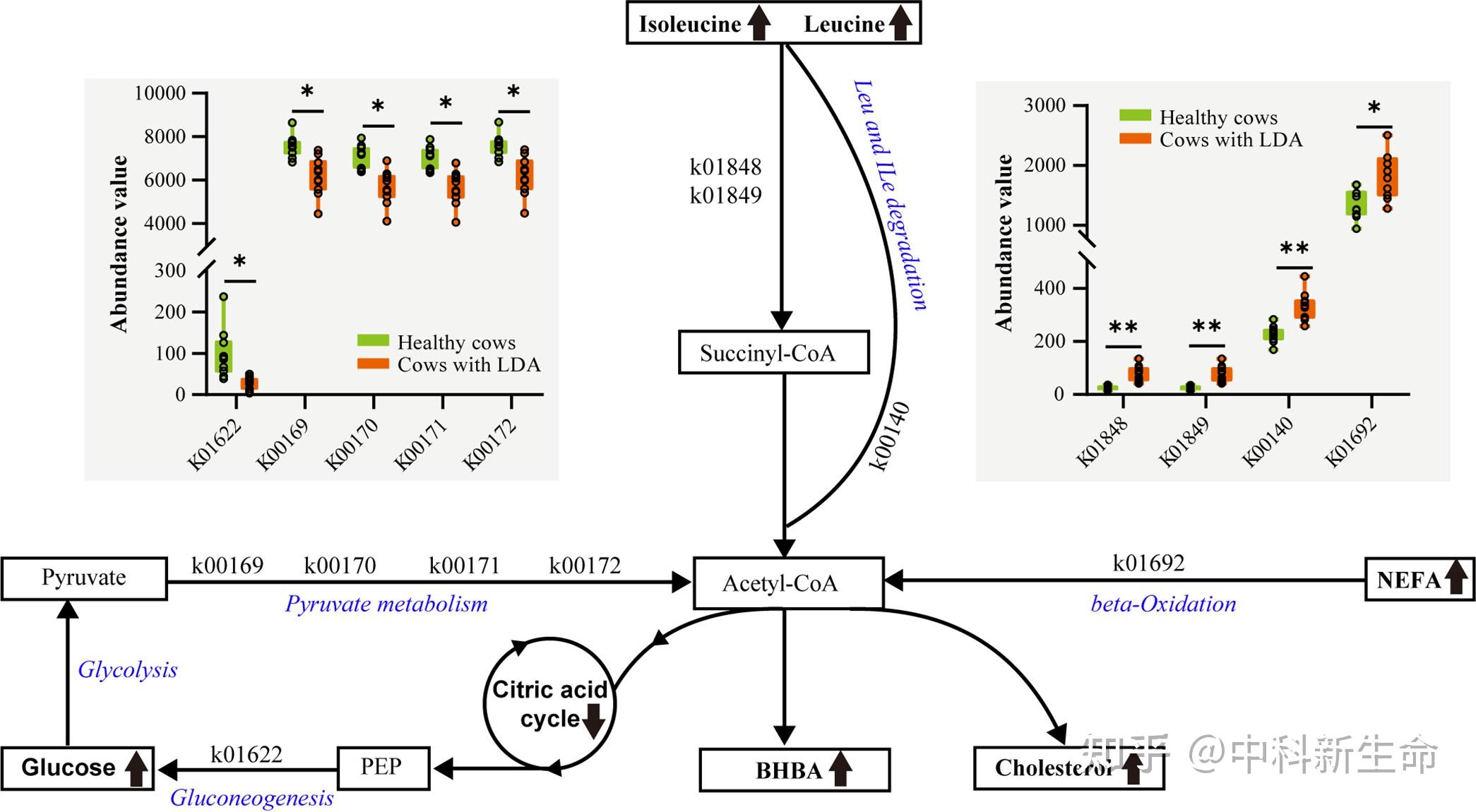
小编小结
本研究利用多组学数据综合分析了LDA对奶牛肠道菌群、代谢产物和宿主表型的影响。研究结果清楚地表明,LDA奶牛的肠道菌群失调状态与氨基酸缺乏症有关。在LDA的背景下,肠道微生物组成的变化与酮生成和葡萄糖代谢密切相关。此外,研究者还发现了与LDA相关的关键代谢产物。本研究为LDA发病机制研究提供了新的思路,也为LDA的预防和治疗奠定了理论基础。
中科优品推荐
中科新生命16S+代谢完整打包产品可以提供多种关联分析结果,多角度、多层次深入的挖掘肠道菌群和代谢物之间的关联性,筛选引起代谢变化的关键菌群。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/163859.html