ArrayDeque接口提供了以上几个方法,使用时要注意:
- 尽量避免Collection的add()和remove()方法,而是要使用offer()来加入元素,使用poll()来获取并移出元素。
- 它们的优点是通过返回值可以判断成功与否,add()和remove()方法在失败的时候会抛出异常。
- 如果要使用队头元素而不移出该元素,使用element()或者peek()方法
- 添加元素:
- 弹出元素:
- 获取栈顶元素但不弹出:
用一个队列来记录树的元素,每次都是弹出父节点,然后加入这个这个节点的所有子节点。没有元素供插入或弹出就跳过
可以参考玩转算法与数据结构的视频教程和代码
- 5-6 层序遍历(广度优先遍历)
- 二叉树层序遍历参考代码
- N叉树层序遍历参考代码
可以参考玩转算法与数据结构的视频教程和代码
- 5-5 二分搜索树的遍历(深度优先遍历)
- 代码
被访问过地节点标记为蓝色(加入过queue队列就认为被访问过),遍历过一个元素即从队列queue弹出元素的动作,遍历结果存到order数组中
讯享网
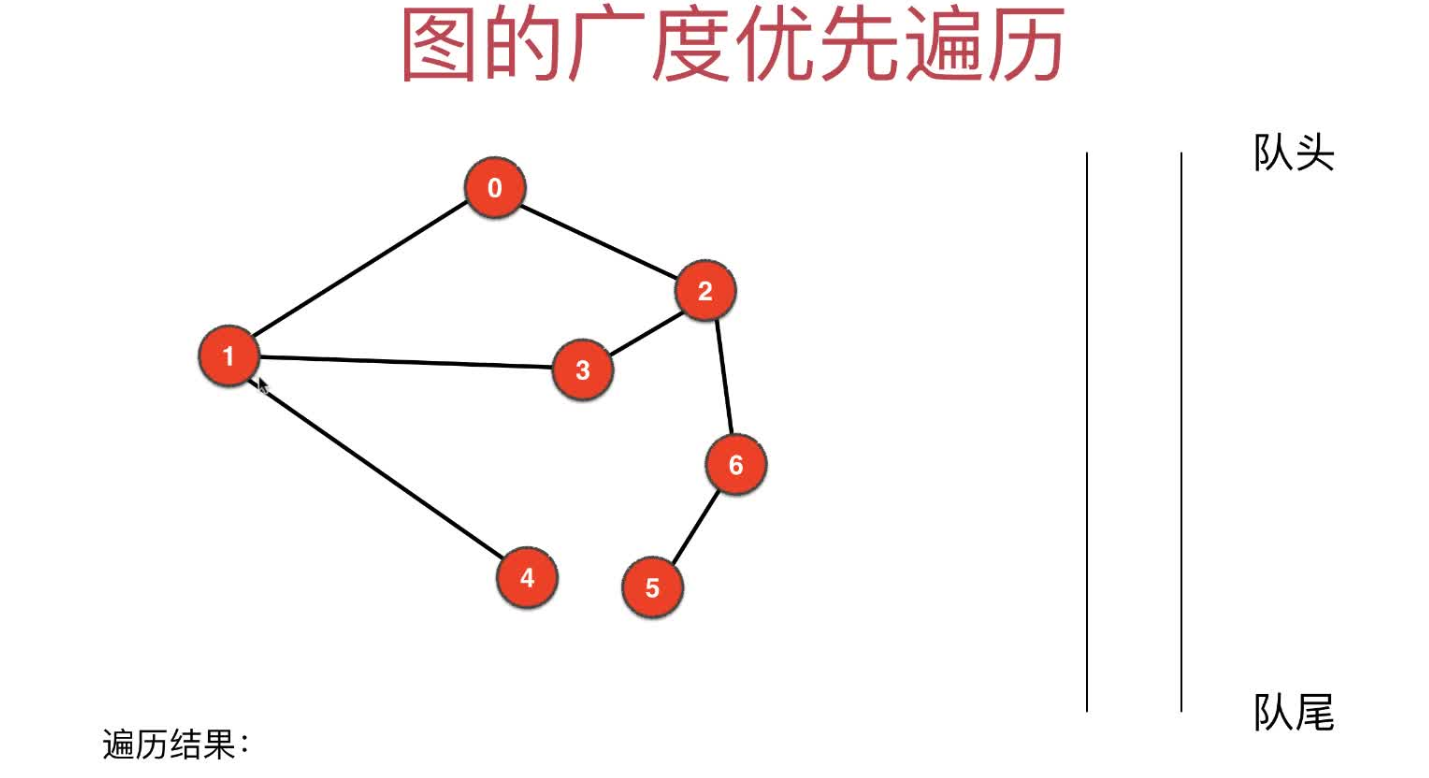
- 1.初始化图,从顶点0开始遍历,当然也可以选其他顶点,这里只为了演示。初始时queue=[],order=[],visited=
- 2.节点0作为起始点,没有父节点,队列此时为空,把节点0加入队列,此时queue=[0],order=[],visited=
- 3.弹出父节点0,欲加入节点0的邻接点1和2,visited[1]和visited[2]均为false所以都加入queue,此时queue=[1, 2], order=[0], visited=
- 4.弹出父节点1,欲加入节点1的邻接点3和4,visited[3]和visited[4]均为false所以都加入queue,此时queue=[2, 3, 4],order=[0, 1],visited=
- 5.弹出父节点2,欲加入节点2的邻接点3和6,因为visited[3]=true,所以只加入6,此时queue=[3, 4, 6],order=[0, 1, 2],visited=
- 6.弹出父节点3,欲加入节点3的邻接点1和2,因为visited[1]和visited[2]均为true,所以都不加入,此时queue=[4, 6],order=[0, 1, 2, 3],visited=
- 7.弹出父节点4,欲加入节点4的邻接点1,因为visited[1]为true,所以不加入,此时queue=[6],order=[0, 1, 2, 3, 4],visited=
- 8.弹出父节点6,欲加入节点6的邻接点2和5,因为visited[2]为true,所以加入5,此时queue=[5],order=[0, 1, 2, 3, 4, 6],visited=
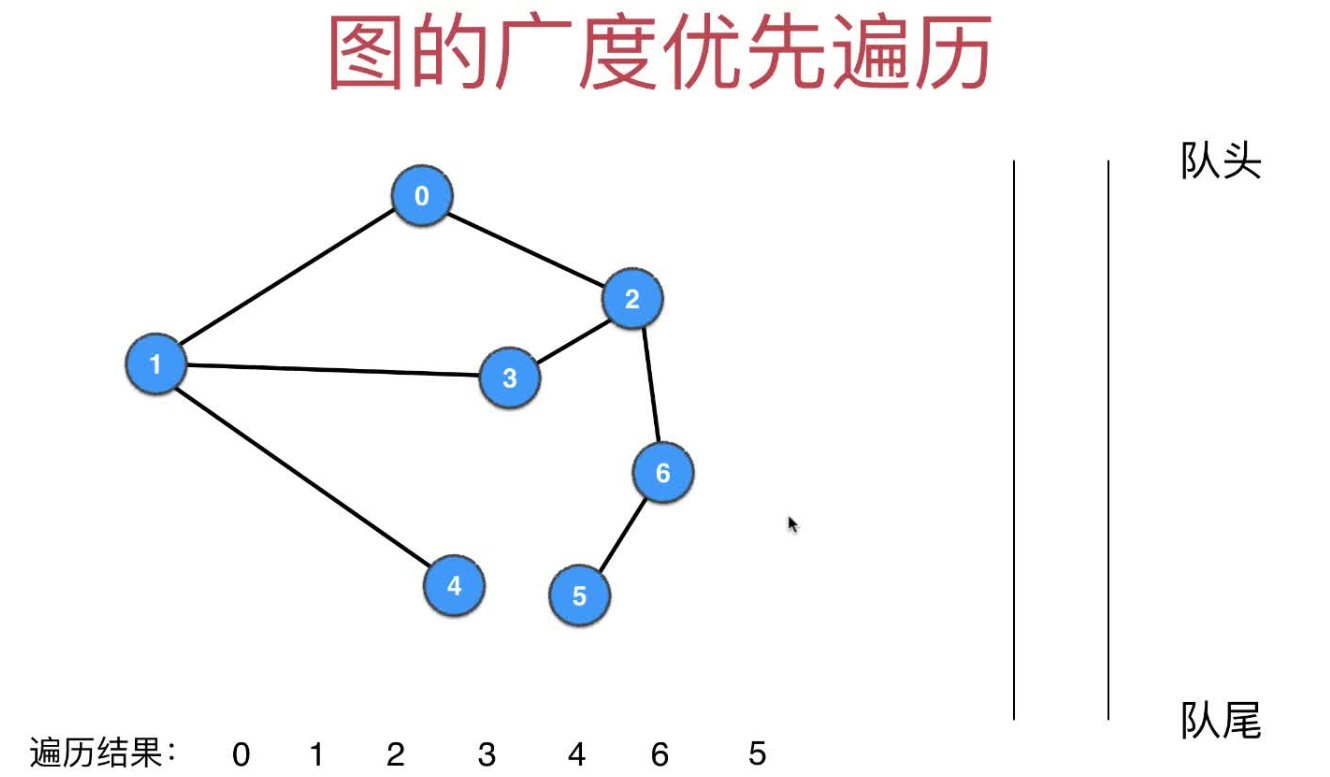
- 9.弹出父节点5,欲加入节点5的邻接点6,因为visited[6]为true,所以不加入,此时queue=[],order=[0, 1, 2, 3, 4, 6, 5],visited=
- 10.队列已经为空,广度优先遍历结束,最终的遍历结果为order=[0, 1, 2, 3, 4, 6, 5]

和树的广度优先遍历完全一样:,此外还需要记录每个节点是否已经被遍历而引入了visited数组
- 实现代码
- 测试代码
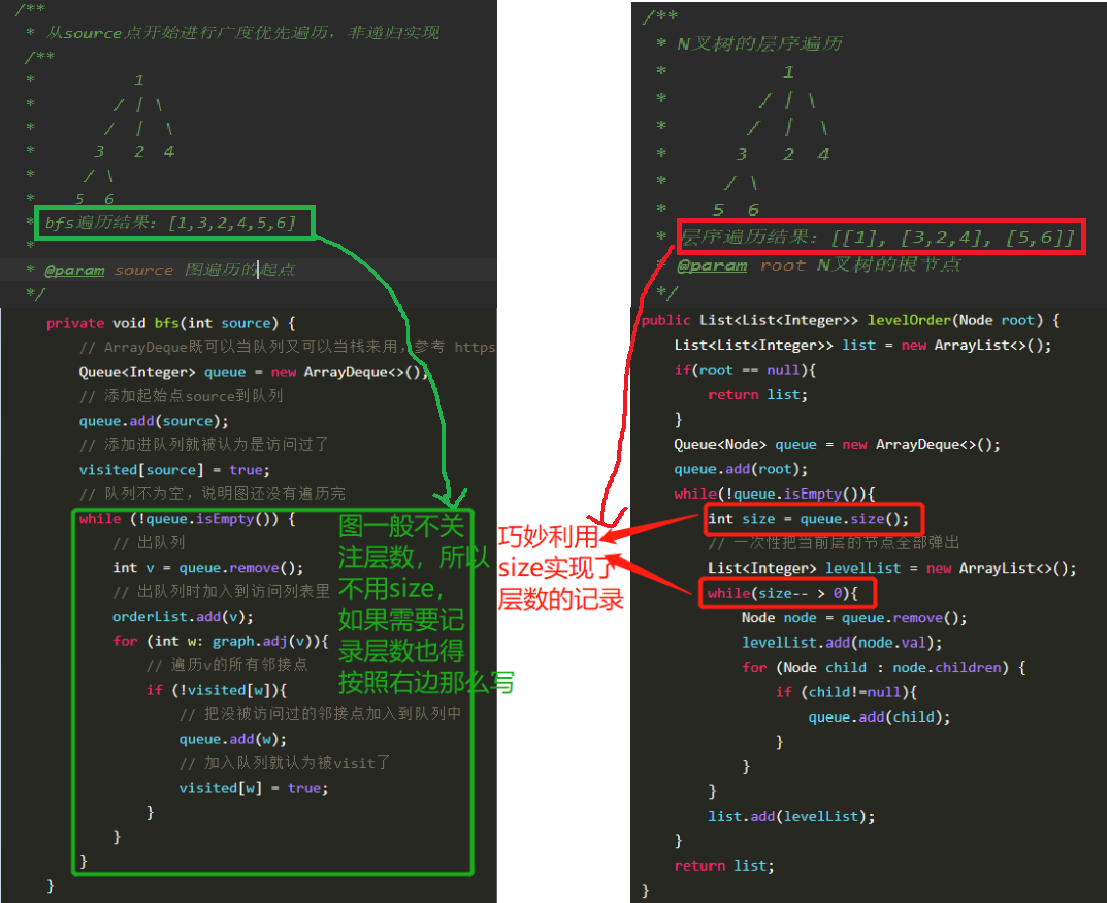
N叉树的层序遍历那里巧妙利用size实现了层次的记录,最后的结果是List的List。BFS需要记录层次时也得这么写,其他的实现方式太麻烦
- N叉树的层序遍历
- 经典的广度优先遍历
__
上一章使用DFS解决地几类问题,使用BFS几乎都可以解决,思路也是一样的,下面几节将进行讲解
参考深度优先遍历的代码
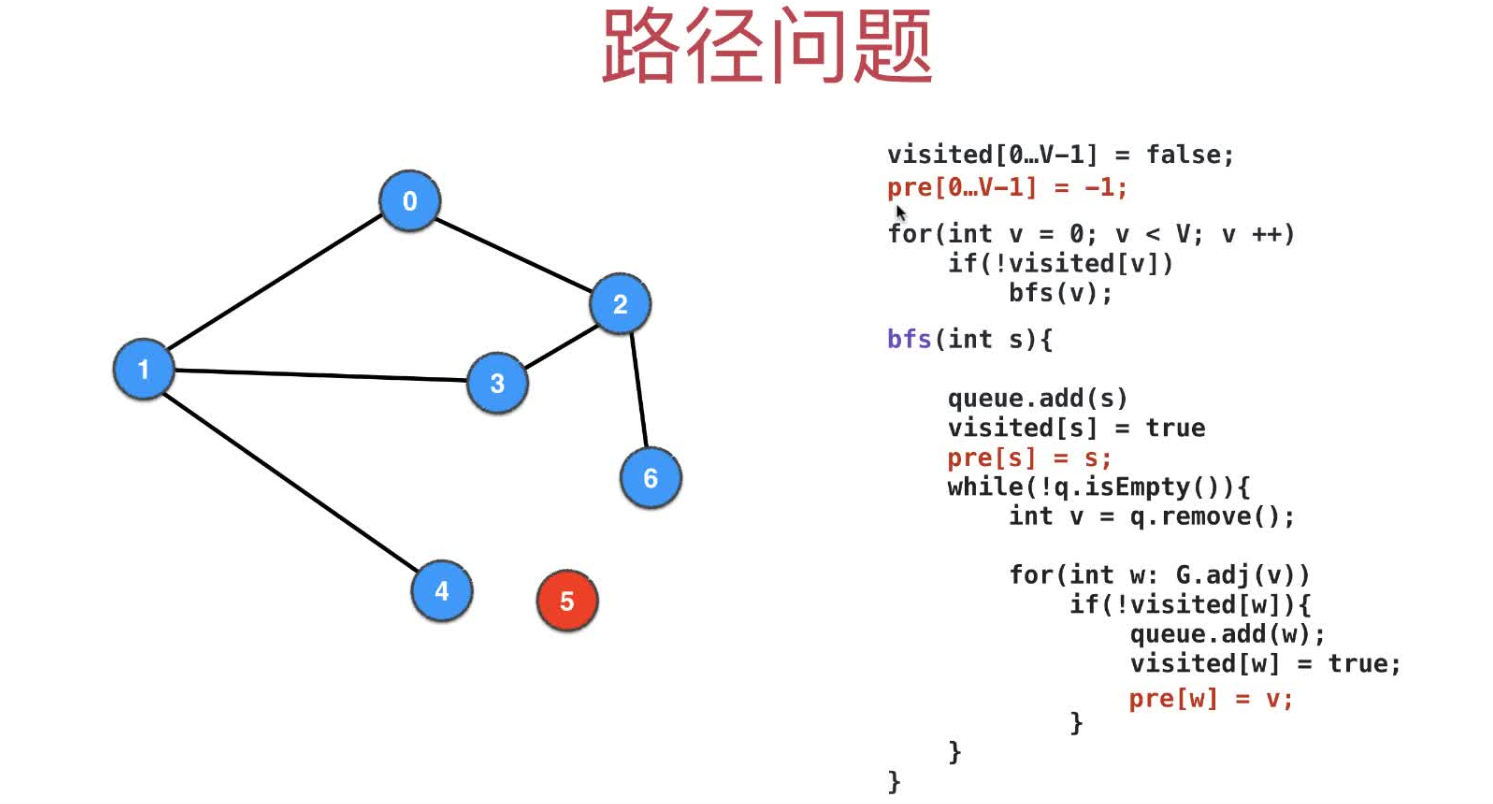
pre记录每个被visited节点的上一个visited节点,从target点开始遍历pre到source,结果逆序即得到路径
- 实现代码
- 测试代码
BFS遍历到target就提前退出,这样可以极大地节省递归的成本,当前图的构造就只是为了求解当前两个点的路径
- 实现代码
- 测试代码
和DFS基本相同
- 实现代码
- 测试代码
和DFS的基本相同
- 实现代码
- 测试代码
和DFS的基本相同
- 实现代码
- 测试代码
实际就是求出了无权图中指定两点的最短路径,还有个小缺点就是只列出了最短路径经过点,而没有列出具体的最短路径的值
- 代码参考
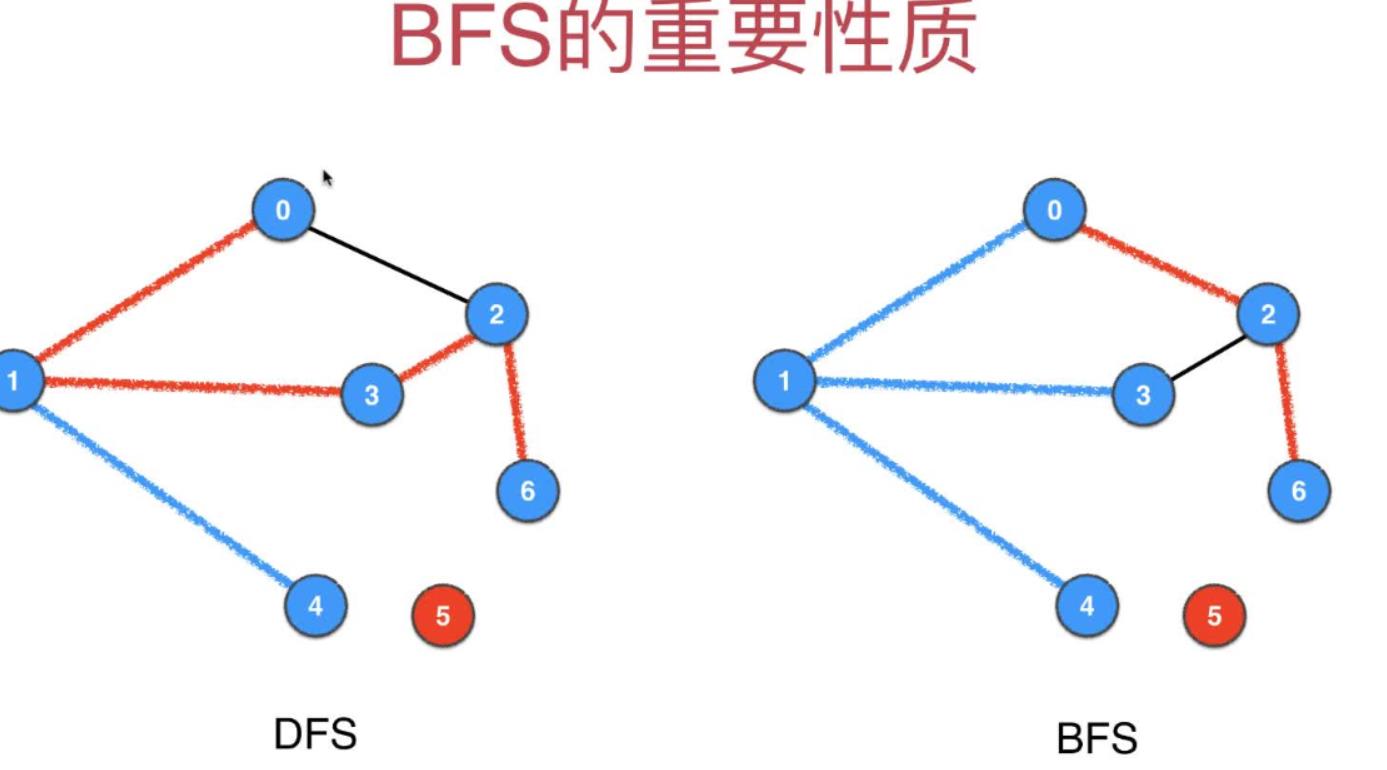
代码的图示如下,左侧是DFS的单源路径问题,右侧是BFS的单源路径问题
ps:
返回最短路径经过的点和最短路径的值,实际就是加了一个distance数组,记录了BFS过程中经过的点到起点source的距离(无权图默认边长是1,经过一条边加1即可)。测试的Graph就是上面的图
- 实现代码
- 测试代码
这个distance数组在LeetCode上的很多BFS的题目都很重要,要好好理解下
- 栈 是先进后出,后加入地点一般都是深层的点,所以越来越往深处走,就成了深度优先遍历
- 队列是先进先出,先加入地点一般都是上层的点,所以越来越往左右走,就成了广度优先遍历
为了方便看,stack和queue添加元素的方法都写成了add,删除元素的方法都写成了remove

下面图的x就是指存储遍历点的容器类型,当是Stack时就是深度优先遍历,当是Queue时就是广度优先遍历,其实也可以是其他的容器类型,比如是个随机弹出的容器类型,那么遍历就相当于是随机遍历了,这个思想在刘老师的《看地见的算法 7个经典应用诠释算法精髓》里有应用到

DFS的递归实现中的实际就是起到栈的作用


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/144059.html