<div id="navCategory"></div> 讯享网
图的深度优先搜索(Depth First Search) .
1) 深度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,深度优先遍历的策略就是首先访问第一个邻接结点,然后再以这个被访问的邻接结点作为初始结点,访问它的第一个邻接结点,可以这样理解:每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
2)我们可以看到,这样的访问策略是优先往纵向挖掘深入而不是对一个结点的所有邻接结点进行横向访问。
3)显然,深度优先搜索是一个递归的过程(可以用栈来模拟)
例如这个图进行深度优先遍历:V1--->V2--->V5--->V3--->V6-->V4
具体的代码实现
图的广度优先搜索(Breadth First Search) .
1)广度优先遍历,从初始访问结点出发,初始访问结点可能有多个邻接结点,广度优先遍历的策略就是首先访问第一个邻接结点,然后依次访问初始访问结点的相邻接点,然后访问初始节点的第一个邻接结点的邻接顶点,初始节点第二个邻接结点的邻接节点.....,
2)广度优先遍历需要使用一个队列以保持访问过的结点的顺序,以便按这个顺序来访问这些结点的邻接结点
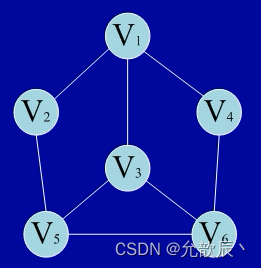
例如这个图进行广度优先遍历:V1--->V2--->V4--->V5--->V6-->V3
具体的代码实现

有一幅以的二维整数数组表示的图画,其中表示该图画的像素值大小。
你也被给予三个整数 , 和 。你应该从像素开始对图像进行 上色填充 。
为了完成 上色工作 ,从初始像素开始,记录初始坐标的 上下左右四个方向上 像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应 四个方向上 像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为。
最后返回 经过上色渲染后的图像。
力扣: 力扣
这是一道典型的BFS和DFS的问题,
先来考虑广度优先遍历的方法:我们可以先把初始点像素相同的的上下左右点全部涂完色,然后再把第一次涂上色的格子的上下左右点涂上色,以此类推,直到没有可以涂色的格子
假设所有格子都可以涂色,那么广度优先的涂色顺序如下图所示进行涂色处理,这个过程中我们需要使用一个队列进行模拟,每一次寻找上下左右可以涂色的位置(不越界,像素值相同)进行涂色,并且入队列,把像素值替换为color
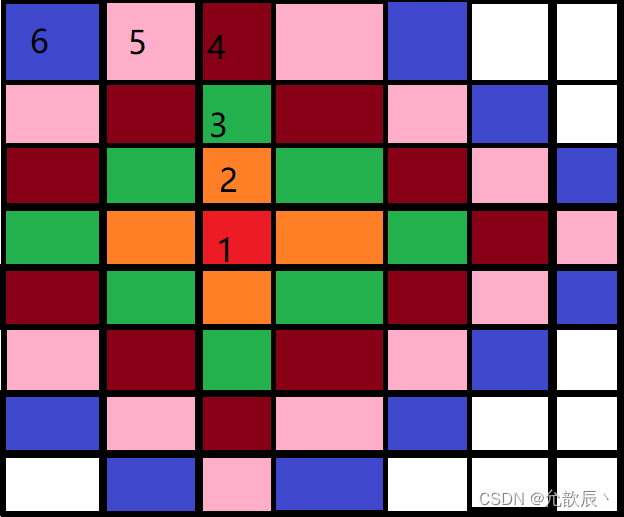
再来考虑深度优先遍历,深度优先遍历自然就是使用递归来实现,每一次我们访问上方的格子(默认的访问顺序是上下左右),直到不能访问,然后访问不能访问上班的格子的下边的格子,此格子不能访问再访问左边格子,不能访问再访问右边格子,一层一层的递归下去.......
1.广度优先遍历
2.深度优先遍历
给你一个大小为 的二进制矩阵 。
岛屿是由一些相邻的(代表土地) 构成的组合,这里的「相邻」要求两个 必须在 水平或者竖直的四个方向上 相邻。你可以假设 的四个边缘都被 (代表水)包围着。
岛屿的面积是岛上值为 的单元格的数目。

计算并返回 中最大的岛屿面积。如果没有岛屿,则返回面积为 。
力扣:力扣
这一题上一题相似,上一题是把像素相同的格子全部涂上颜色,这一题是寻找面积最大的岛屿,把能涂的格子全部涂上颜色,这一题是把一个岛屿的面积全部遍历从而求出面积,在给出的海域中有很多的岛屿,我们只需要每次记录面积最大的岛屿的面积,最后直接返回即可
广度优先遍历:遍历整个矩阵grid,找到为陆地(1),然后在这片陆地上进行遍历,把遍历到的陆地格子置为0,也就是海洋,队列中没有陆地格子了,说明这个岛屿全部都遍历完了,和记录的最大面积对比,最终直到全部的矩阵格子遍历完成,返回最大的面积
深度优先遍历:和广度优先的思路一样,唯一不一样的点就是找到岛屿后的遍历顺序,具体看代码
1.广度优先遍历
2.深度优先遍历
给定一个 的二维网格地图 ,其中: 表示陆地, 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
力扣:力扣
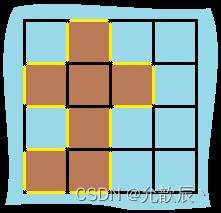
求面积我们可以求出来,但是求周长确实不容易想出来.但是经过我们仔细观察,我们就可以发现,如果岛屿的一边是水或者是边界地区的话,那么这一条边就可以作为周长的一部分(周长+1)
广度优先遍历:这一道题使用这个方法,没必要创建队列,我们只需要把这个二维数组遍历完成,判断每一块陆地的周长,这样我们就可以求出总的边长了,如果这一道题是有很多个岛屿,求周长最大的岛屿的周长,我们还是需要用到队列的
深度优先遍历:深度优先遍历和上边的几题一样的思路,具体看代码
1.广度优先遍历
2.深度优先遍历
到此这篇关于Java实现深度优先搜索(DFS)和广度优先搜索(BFS)算法的文章就介绍到这了,更多相关Java深度优先和广度优先内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容,请联系我们,一经查实,本站将立刻删除。
如需转载请保留出处:https://51itzy.com/kjqy/141966.html