大家好，我是讯享网，很高兴认识大家。

FTT从入门到自闭

0.基本定义

FFT全称(Fast Fourier Transformation)

中文名：快速傅里叶离散变换

作用是能以$O(nlogn)$　计算多项式乘法。

$n$​次多项式：$F(x)=ax^n+bx{n-1}+cx^{n-2}\dots $

$F[i]$​ 表示$F(x)$的$i$次项系数。​

$F(x)=\sum _{i=0}^{n}F[i]x^i$​

---

乘法的本质(卷积)

两个$n$次多项式$A(x),B(x)$相乘。

$C=A\ast B$

$C[k]=\sum _{i=0}^{k}A[i]B[k-i]=\sum _{i+j=k}A[i]B[j]$​

因此乘法的本质就是加法卷积。

---

暴力卷积

P3803 【模板】多项式乘法（FFT）

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=1e6+5; int n,m; ll a[N],b[N],c[N]; void mul(ll *a,ll *b,ll *c){ 
    for(int k=0;k<=n+m;k++) for(int i=0;i<=k;i++) c[k]+=a[i]*b[k-i]; } int main(){ 
    scanf("%d%d",&n,&m); for(int i=0;i<=n;i++) scanf("%lld",&a[i]); for(int i=0;i<=m;i++) scanf("%lld",&b[i]); mul(a,b,c); for(int i=0;i<=n+m;i++) printf("%lld ",c[i]);printf("\n"); return 0; } 

讯享网

1.DFT&IDFT

用$n+1$​个点值(有序数对) 可以唯一确定一个$n$次多项式。

讯享网

因此便有了$FFT$的算法流程：

把系数表达转换为点值表达$\Rightarrow$ 点值表达相乘 $\Rightarrow$ 点值表达转换为系数表达。

把系数表达转换为点值表达”的算法叫做DFT

把点值表达转换为系数表达”的算法叫做IDFT(DFT的逆运算)

• 从一个多项式的系数表达确定其点值表达的过程称为求值(毕竟求点值表达的过程就是取了 n 个 x 然后扔进了多项式求了 n 个值出来);
• 而求值运算的逆运算(也就是从一个多项式的点值表达确定其系数表达)被称为插值.

总结

在平面直角坐标系中,给你(n+1)个点就能确定一个n次多项式(函数)。

点值表示相乘(点乘)远快于暴力卷积。

---

2.单位根(复数)及其性质

关于复数

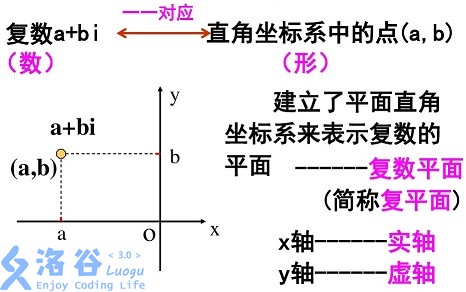
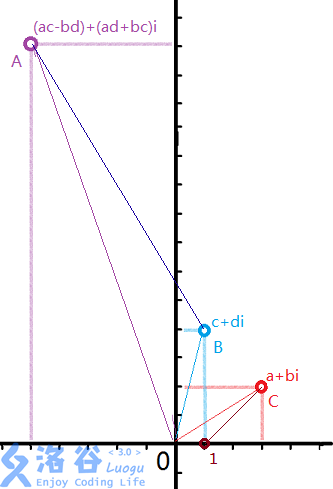
复数相乘时,模长相乘,幅角相加！

---

单位根

看起来很高大上,这是傅里叶快速变换的重要内容。

• n次单位根(n为正整数)是n次幂为1的复数。

换句话说,就是方程$x^n=1$的复数解。

---

单位根的性质

• ${\omega }_n^0=1$
• ${\omega }_n^k=({\omega }_n^1{)}^k$
• ${\omega }_n^j\ast {\omega }_n^k={\omega }_n^{j+k}$
• ${\omega }_{2n}^{2k}={\omega }_n^k$
• 若$n$为偶数，${\omega }_n^{k+n/2}=-{\omega }_n^k$​

总结

复数把数轴扩展到了复平面上,复数可以对应复平面上一个点。

复数也有四则运算。复数相乘时,模长相乘,幅角相加。

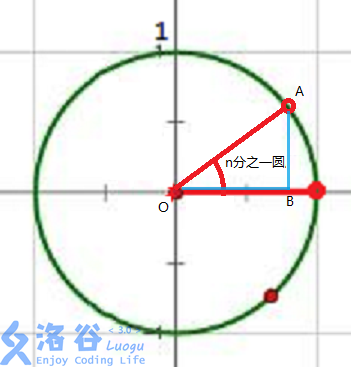
n次单位根(n为正整数)是n次幂为1的复数。

把单位根画到单位圆上之后,就能整出一些性质。

---

3.DFT的加速版本

$F(w_n^k)=FL(w_{n/2}^k)+w_n^{k}FR(w_{n/2}^k)$

$F(w_n^{k+n/2})=FL(w_{n/2}^k)-w_n^{k}FR(w_{n/2}^k)$​

---

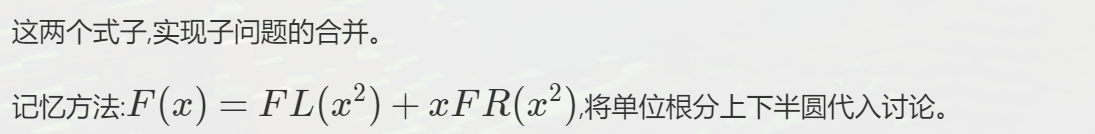
4.DFT的代码实现

还有一个小细节。

上文有一句话：“保证n是2的整幂,不会出现分得不均匀的情况。”

实际应用中,$n$不一定是$2$的正整数次幂。

我们可以补项,在最高次强行添加一些系数为0的项(类似于高精度补0)。不影响我们的计算结果,却占了位置。(具体见代码)

讲完了这些我们可以开始写$DFT$了

1.复数结构体

讯享网#include <iostream> using namespace std; struct CP { 
    CP (double xx=0,double yy=0){ 
   x=xx,y=yy;} double x,y; CP operator + (CP const &B) const { 
   return CP(x+B.x,y+B.y);} CP operator - (CP const &B) const { 
   return CP(x-B.x,y-B.y);} CP operator * (CP const &B) const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} CP operator / (CP const &B) const { 
    double t=B.x*B.x+B.y*B.y; return CP((x*B.x+y*B.y)/t, (y*B.x-x*B.y)/t); } }a,b; int main() { 
    cin>>a.x>>a.y>>b.x>>b.y; CP c; c=a+b; cout<<'('<<c.x<<','<<c.y<<")\n"; c=a-b; cout<<'('<<c.x<<','<<c.y<<")\n"; c=a*b; cout<<'('<<c.x<<','<<c.y<<")\n"; c=a/b; cout<<'('<<c.x<<','<<c.y<<")\n"; return 0; } 

代码

#include<cstdio> #include<cmath> #define Maxn  //用这句话能得到得到精确的π,可以当做结论来记 const double Pi=acos(-1); using namespace std; struct CP { 
    CP (double xx=0,double yy=0){ 
   x=xx,y=yy;} double x,y; CP operator + (CP const &B) const { 
   return CP(x+B.x,y+B.y);} CP operator - (CP const &B) const { 
   return CP(x-B.x,y-B.y);} CP operator * (CP const &B) const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} //除法没用 }w[Maxn]; //w长得是不是很像ω? int n; int main() { 
    scanf("%d",&n); CP sav(cos(2*Pi/n),sin(2*Pi/n)),buf(1,0); for (int i=0;i<n;i++){ 
    w[i]=buf; buf=buf*sav; } for (int i=0;i<n;i++) printf("w[%d][n]=(%.4lf,%.4lf)\n",i,w[i].x,w[i].y); //由于精度问题会出现-0.0000的情况,将就看吧 return 0; } 

递归DFT(简单版本)

讯享网#include <cstdio> #include <cmath> #define Maxn  using namespace std; const double Pi=acos(-1); int n,m; struct CP { 
    CP (double xx=0,double yy=0){ 
   x=xx,y=yy;} double x,y; CP operator + (CP const &B) const { 
   return CP(x+B.x,y+B.y);} CP operator - (CP const &B) const { 
   return CP(x-B.x,y-B.y);} CP operator * (CP const &B) const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} //除法没用 }f[Maxn<<1],sav[Maxn<<1]; void dft(CP *f,int len) { 
    if (len==1)return ;//边界 //指针的使用比较巧妙  CP *fl=f,*fr=f+len/2; for (int k=0;k<len;k++)sav[k]=f[k]; for (int k=0;k<len/2;k++)//分奇偶打乱 { 
   fl[k]=sav[k<<1];fr[k]=sav[k<<1|1];} dft(fl,len/2); dft(fr,len/2);//处理子问题 //由于每次使用的单位根次数不同(len次单位根),所以要重新求。 CP tG(cos(2*Pi/len),sin(2*Pi/len)),buf(1,0); for (int k=0;k<len/2;k++){ 
    //这里buf = (len次单位根的第k个)  sav[k]=fl[k]+buf*fr[k];//(1) sav[k+len/2]=fl[k]-buf*fr[k];//(2) //这两条语句具体见Tips的式子 buf=buf*tG;//得到下一个单位根。 }for (int k=0;k<len;k++)f[k]=sav[k]; } int main() { 
    scanf("%d",&n); for (int i=0;i<n;i++)scanf("%lf",&f[i].x); //一开始都是实数,虚部为0 for(m=1;m<n;m<<=1); //把长度补到2的幂,不必担心高次项的系数,因为默认为0 dft(f,m); for(int i=0;i<m;++i) printf("(%.4f,%.4f)\n",f[i].x,f[i].y); return 0; } 

现在问题来了,DFT输出的都是些杂乱的点值表达,所以解决不了问题。

上文说过,IDFT是$DFT$的逆(CP),她可以把点值还原成多项式,最终完成乘法。

现在到了讲$IDFT$的时候了!!!

5.IDFT理论与FFT初步实现

FFT的初步版本

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=2.7e6+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7; const double PI=acos(-1); #define mst(a) memset(a,0,sizeof a) #define lx x<<1 #define rx x<<1|1 #define reg register #define PII pair<int,int> #define fi first #define se second #define pb push_back int n,m; struct CP{ 
    //Complex 的加减乘除运算.  CP (double xx=0,double yy=0){ 
   x=xx,y=yy;} double x,y; CP operator + (CP const &B) const { 
   return CP(x+B.x,y+B.y);} CP operator - (CP const &B) const { 
   return CP(x-B.x,y-B.y);} CP operator * (CP const &B) const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} }f[N],p[N],sav[N]; void fft(CP *f,int len,bool flag) //分治解决.  { 
    if (len==1) return;//len==1 是常数直接返回.  CP *fl=f,*fr=f+(len>>1);//递归处理fl,fr.  for (int k=0;k<len;k++)sav[k]=f[k];//储存起来.  for (int k=0;k<len/2;k++) //分奇偶处理.  { 
   fl[k]=sav[k<<1];fr[k]=sav[k<<1|1];} fft(fl,len>>1,flag);//递归解决.  fft(fr,len>>1,flag); CP tG(cos(2*PI/len),sin(2*PI/len)),buf(1,0);//W(len,0).  if (!flag)tG.y*=-1; for (int k=0;k<len/2;k++){ 
    CP tmp=buf*fr[k]; sav[k]=fl[k]+tmp; //公式.  sav[k+len/2]=fl[k]-tmp; buf=buf*tG; }for (int k=0;k<len;k++)f[k]=sav[k]; } int main(){ 
    scanf("%d%d",&n,&m); for (int i=0;i<=n;i++)scanf("%lf",&f[i].x); for (int i=0;i<=m;i++)scanf("%lf",&p[i].x); for(m+=n,n=1;n<=m;n<<=1);//把长度补到2的幂 fft(f,n,1);fft(p,n,1);//DFT for(int i=0;i<n;++i)f[i]=f[i]*p[i]; fft(f,n,0);//FFT for(int i=0;i<=m;++i)printf("%d ",(int)(f[i].x/n+0.49)); return 0; } 

蝴蝶操作+位运算优化的递归版。

讯享网#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N=2.7e6+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7; const double PI=acos(-1); #define mst(a) memset(a,0,sizeof a) #define lx x<<1 #define rx x<<1|1 #define reg register #define PII pair<int,int> #define fi first #define se second #define pb push_back int n,m; struct CP{ 
    //Complex 的加减乘除运算.  CP (double xx=0,double yy=0){ 
   x=xx,y=yy;} double x,y; CP operator + (CP const &B) const { 
   return CP(x+B.x,y+B.y);} CP operator - (CP const &B) const { 
   return CP(x-B.x,y-B.y);} CP operator * (CP const &B) const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} }f[N],p[N]; void fft(CP *f,int len,bool flag) //分治解决.  { 
    if (len==1) return;//len==1 是常数直接返回.  fft(f,len/2,flag); fft(f+len/2,len/2,flag); CP tG(cos(2*PI/len),sin(2*PI/len)),buf(1,0);//W(len,0).  if (!flag)tG.y*=-1; for (int k=0;k<(len>>1);k++){ 
    CP tmp=buf*f[k+(len>>1)]; f[k+(len>>1)]=f[k]-tmp; //公式.  f[k]=f[k]+tmp; buf=buf*tG; } } int tr[N]; int main(){ 
    scanf("%d%d",&n,&m); for (reg int i=0;i<=n;i++)scanf("%lf",&f[i].x); for (reg int i=0;i<=m;i++)scanf("%lf",&p[i].x); for(m+=n,n=1;n<=m;n<<=1);//把长度补到2的幂 for(reg int i=0;i<n;i++) tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0); //蝴蝶操作.  for (reg int i=0;i<n;i++) //预先处理反转序列.  if (i<tr[i])swap(f[i],f[tr[i]]);//只交换一次.  for (reg int i=0;i<n;i++) if (i<tr[i])swap(p[i],p[tr[i]]);//同上.  fft(f,n,1);fft(p,n,1);//DFT for(reg int i=0;i<n;++i)f[i]=f[i]*p[i]; for (int i=0;i<n;i++) if (i<tr[i])swap(f[i],f[tr[i]]); fft(f,n,0);//FFT for(reg int i=0;i<=m;++i)printf("%d ",(int)(f[i].x/n+0.49)); return 0; } 

迭代版

#include<cstdio> #include<cmath> #include<algorithm> using namespace std; typedef long long ll; const int N=2.7e6+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7; const double PI=acos(-1); #define mst(a) memset(a,0,sizeof a) #define lx x<<1 #define rx x<<1|1 #define reg register #define PII pair<int,int> #define fi first #define se second #define pb push_back int n,m; struct CP { 
    CP (double xx=0,double yy=0){ 
   x=xx,y=yy;} double x,y; CP operator + (CP const &B) const { 
   return CP(x+B.x,y+B.y);} CP operator - (CP const &B) const { 
   return CP(x-B.x,y-B.y);} CP operator * (CP const &B) const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} }f[N],p[N]; int tr[N]; void fft(CP *f,bool flag) { 
    for (reg int i=0;i<n;i++) if (i<tr[i])swap(f[i],f[tr[i]]); //枚举区间长度  for(reg int p=2;p<=n;p<<=1){ 
    int len=p>>1;//待合并的长度 CP tG(cos(2*PI/p),sin(2*PI/p)); if(!flag)tG.y*=-1;//p次单位根 for(reg int k=0;k<n;k+=p){ 
   //枚举起始点  CP buf(1,0);//遍历一个子问题并合并 for(reg int l=k;l<k+len;l++){ 
    CP tt=buf*f[len+l]; f[len+l]=f[l]-tt; f[l]=f[l]+tt; buf=buf*tG; } } } } int main() { 
    scanf("%d%d",&n,&m); for (reg int i=0;i<=n;i++)scanf("%lf",&f[i].x); for (reg int i=0;i<=m;i++)scanf("%lf",&p[i].x); for(m+=n,n=1;n<=m;n<<=1); for(reg int i=0;i<n;i++) tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0); fft(f,1);fft(p,1);//DFT for(reg int i=0;i<n;++i)f[i]=f[i]*p[i]; fft(f,0); for(reg int i=0;i<=m;++i)printf("%d ",(int)(f[i].x/n+0.49)); return 0; } 

6.FFT习题

P1919 【模板】A*B Problem升级版

将每位成多项式的系数

则有：$12345=5\times 10^0+4\times 10^1+3\times 10^2+2\times 10^3+1\times 10^4$

即：$f(x)=12345$为$4$次多项式。

然后乘法就是两个多项式的乘积，上$FFT$​得到结果，然后按照高精的进位方式并去前导零即可。

时间复杂度：$O(nlogn)$

讯享网#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef unsigned long long ull; const int N=3e6+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7; #define mst(a,b) memset(a,b,sizeof a) #define PII pair<int,int> #define fi first #define se second #define pb emplace_back #define SZ(a) (int)a.size() #define IOS ios::sync_with_stdio(false),cin.tie(0)  void Print(int *a,int n){ 
    for(int i=1;i<n;i++) printf("%d ",a[i]); printf("%d\n",a[n]); } #define rgi register int const double PI=acos(-1); struct CP{ 
    CP (double x=0,double y=0):x(x),y(y){ 
   } double x,y; CP operator +(CP const &B)const { 
   return CP(x+B.x,y+B.y);} CP operator -(CP const &B)const { 
   return CP(x-B.x,y-B.y);} CP operator *(CP const &B)const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} }A[N],B[N]; int tr[N],n,m; void fft(CP *f,bool flag){ 
    for(rgi i=0;i<n;i++) if(i<tr[i]) swap(f[i],f[tr[i]]);//蝴蝶变换 for(rgi p=2,len=1;p<=n;p<<=1,len<<=1){ 
    //枚举区间长度 CP tG(cos(2*PI/p),sin(2*PI/p));if(!flag) tG.y*=-1;//p次单位根 for(rgi k=0;k<n;k+=p){ 
    //枚举起点 CP buf(1,0); for(rgi l=k;l<k+len;l++){ 
    //合并区间 CP tt=buf*f[len+l]; f[len+l]=f[l]-tt; f[l]=f[l]+tt; buf=buf*tG; } } } } inline void init(int &n,int m){ 
    for(n=1;n<=m;n<<=1); for(rgi i=0;i<n;i++) tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0); } char a[N],b[N]; int ans[N<<1]; int main() { 
    scanf("%s%s",a,b); int la=strlen(a),lb=strlen(b); for(int i=la-1;~i;i--) A[la-i-1]=a[i]-'0'; for(int i=lb-1;~i;i--) B[lb-i-1]=b[i]-'0'; m=la+lb; init(n,m); fft(A,1),fft(B,1); for(int i=0;i<=n;i++) A[i]=A[i]*B[i]; fft(A,0); for(int i=0;i<=n;i++){ 
    ans[i]+=(int)(A[i].x/n+0.5); if(ans[i]>=10) ans[i+1]+=ans[i]/10,ans[i]%=10,n+=(i==n); } while(!ans[n]&&n>1) n--; while(~n) printf("%d",ans[n--]); return 0; } 

---

P3338 [ZJOI2014]力

令$g_i=\frac{1}{i^2},q_0=0,g_0=0$​

左边$=\sum _{i=1}^{j-1}{q}_i\times g_{j-i}=\sum _{i=0}^j{q}_i\times g_{j-i}$​

右边$=\sum _{i=j}^n{q}_i\times g_{i-j}=\sum _{i=0}^{n-j}{q}_{i+j}{g}_i=\sum _{i=0}^{n-j}{q}_{i+j}{g}_i$​​

令$q_i=f_{n-i}$

右边$=\sum _{i=0}^{n-j}{f}_{n-j-i}{g}_i=\sum _{i=0}^t{f}_{t-i}{g}_i$

这样就都化成了卷积的形式。

然后就可以上FFT了。

// Problem: P3338 [ZJOI2014]力 // Contest: Luogu // URL: https://www.luogu.com.cn/problem/P3338 // Memory Limit: 125 MB // Time Limit: 3000 ms // Date: 2021-07-30 14:55:52 // --------by Herio-------- #include<bits/stdc++.h> using namespace std; typedef long long ll; typedef unsigned long long ull; const int N=3e5+5,M=2e4+5,inf=0x3f3f3f3f,mod=1e9+7; #define mst(a,b) memset(a,b,sizeof a) #define PII pair<int,int> #define fi first #define se second #define pb emplace_back #define SZ(a) (int)a.size() #define IOS ios::sync_with_stdio(false),cin.tie(0)  void Print(int *a,int n){ 
    for(int i=1;i<n;i++) printf("%d ",a[i]); printf("%d\n",a[n]); } #define rgi register int const double PI=acos(-1); struct CP{ 
    CP (double x=0,double y=0):x(x),y(y){ 
   } double x,y; CP operator +(CP const &B)const { 
   return CP(x+B.x,y+B.y);} CP operator -(CP const &B)const { 
   return CP(x-B.x,y-B.y);} CP operator *(CP const &B)const { 
   return CP(x*B.x-y*B.y,x*B.y+y*B.x);} }A[N],B[N],C[N]; int tr[N],n,m,li; void fft(CP *f,bool flag){ 
   //flag=1 DFT flag=0 IDFT for(rgi i=0;i<li;i++) if(i<tr[i]) swap(f[i],f[tr[i]]);//蝴蝶变换 for(rgi p=2,len=1;p<=li;p<<=1,len<<=1){ 
    //枚举区间长度 CP tG(cos(2*PI/p),sin(2*PI/p));if(!flag) tG.y*=-1;//p次单位根 for(rgi k=0;k<li;k+=p){ 
    //枚举起点 CP buf(1,0); for(rgi l=k;l<k+len;l++){ 
    //合并区间 CP tt=buf*f[len+l]; f[len+l]=f[l]-tt; f[l]=f[l]+tt; buf=buf*tG; } } } if(!flag) for(rgi i=0;i<li;i++) f[i].x/=li; } inline void init(int &li,int m){ 
    for(li=1;li<=m;li<<=1); for(rgi i=0;i<li;i++) tr[i]=(tr[i>>1]>>1)|((i&1)?li>>1:0); } int main(){ 
    scanf("%d",&n); for(rgi i=1;i<=n;i++){ 
    scanf("%lf",&A[i].x); C[n-i].x=A[i].x; B[i].x=(double)(1.0/i/i); } init(li,n<<1); fft(A,1),fft(B,1),fft(C,1); for(int i=0;i<li;i++) A[i]=A[i]*B[i],C[i]=C[i]*B[i]; fft(A,0),fft(C,0); for(rgi i=1;i<=n;i++) printf("%.3f\n",A[i].x-C[n-i].x); return 0; } 

参考文章

传送门